题目内容
 如图,把一个矩形纸片ABCD沿AD和BC的中点连线EF对折,要使矩形AEFB与原矩形相似,则原矩形长与宽的比为
如图,把一个矩形纸片ABCD沿AD和BC的中点连线EF对折,要使矩形AEFB与原矩形相似,则原矩形长与宽的比为分析:根据相似多边形对应边的比相等,设出原来矩形的长与宽,就可得到一个方程,解方程即可求得.
解答:解:根据条件可知:矩形AEFB∽矩形ABCD.
∴
=
.
设AD=x,AB=y,则AE=
x.则
=
,即:
x2=y2.
∴
=2.
∴x:y=
:1.
即原矩形长与宽的比为
:1.
故答案为:
:1.
∴
| AE |
| AB |
| AB |
| AD |
设AD=x,AB=y,则AE=
| 1 |
| 2 |
| ||
| y |
| y |
| x |
| 1 |
| 2 |
∴
| x2 |
| y2 |
∴x:y=
| 2 |
即原矩形长与宽的比为
| 2 |
故答案为:
| 2 |
点评:本题考查了相似多边形的性质,根据相似形的对应边的比相等,把几何问题转化为方程问题,正确分清对应边,以及正确解方程是解决本题的关键.

练习册系列答案
相关题目
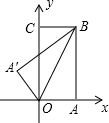 如图,把一个矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在A′的位置上.若OB=
如图,把一个矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在A′的位置上.若OB= 5、如图,把一个矩形纸片ABCD沿EF折叠后,点D、C分别落在D′、C′的位置.若∠EFB=α,则∠AED′等于( )
5、如图,把一个矩形纸片ABCD沿EF折叠后,点D、C分别落在D′、C′的位置.若∠EFB=α,则∠AED′等于( ) 如图,把一个矩形纸片ABCD沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=55°,则∠AED′等于( )
如图,把一个矩形纸片ABCD沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=55°,则∠AED′等于( ) 18、如图,把一个矩形纸片OABC放入平面直角坐标系中,使0A、OC分别落在x轴、y轴上,连接OB,将纸片0ABC沿OB折叠,使点A落在A′的位置上.若0A=10,AB=5,则点A′的坐标为
18、如图,把一个矩形纸片OABC放入平面直角坐标系中,使0A、OC分别落在x轴、y轴上,连接OB,将纸片0ABC沿OB折叠,使点A落在A′的位置上.若0A=10,AB=5,则点A′的坐标为