Question

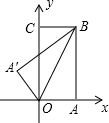
18、如图，把一个矩形纸片OABC放入平面直角坐标系中，使0A、OC分别落在x轴、y轴上，连接OB，将纸片0ABC沿OB折叠，使点A落在A′的位置上．若0A=10，AB=5，则点A′的坐标为

（6，8）

．

Answer 1

分析：过点A'作A'D⊥OA，A'E⊥y轴，设A′的坐标为（x，y），则A'E=x，A'D=y，A'F=y-5，BF=10-x，在Rt△A'FB和Rt△A'OE中，根据勾股定理列方程组求解．

解答：解：过点A'作A'D⊥OA于D，交BC于点F，A'E⊥y轴于E，
设A′的坐标为（x，y），则A'E=x，A'D=y，A'F=y-5，BF=10-x，
根据勾股定理可得
x²+y²=10²，
（y-5）²+（10-x）²=5²，
解得x=6，y=8，
∴点A′的坐标为（6，8）．

点评：此题综合考查了矩形、勾股定理、点的坐标等知识点，难度中等．