题目内容
17.已知抛物线y=a(x+1)(x-$\frac{3}{a}$)与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的a的值有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 整理抛物线解析式,确定出抛物线与x轴的一个交点A和y轴的交点C,然后求出AC的长度,再分①a>0时,点B在x轴正半轴时,分AC=BC、AC=AB、AB=BC三种情况求解;②a<0时,点B在x轴的负半轴时,点B只能在点A的左边,只有AC=AB一种情况列式计算即可.
解答 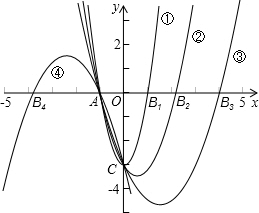 解:解法1:y=a(x+1)(x-$\frac{3}{a}$)=(x+1)(ax-3),
解:解法1:y=a(x+1)(x-$\frac{3}{a}$)=(x+1)(ax-3),
所以,抛物线经过点A(-1,0),C(0,-3),
AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=$\sqrt{1+{3}^{2}}$=$\sqrt{10}$,
点B坐标为($\frac{3}{a}$,0),
①k>0时,点B在x正半轴上,
若AC=BC,则$\sqrt{(\frac{3}{a})^{2}+{3}^{2}}=\sqrt{10}$,解得a=3,
若AC=AB,则$\frac{3}{a}$+1=$\sqrt{10}$,解得a=$\frac{\sqrt{10}+1}{3}$,
若AB=BC,则 $\frac{3}{a}$+1=$\sqrt{(\frac{3}{a})^{2}+{3}^{2}}$,解得a=$\frac{3}{4}$;
②k<0时,点B在x轴的负半轴,点B只能在点A的左侧,
只有AC=AB,则-1-$\frac{3}{a}$=$\sqrt{10}$,解得a=-$\frac{\sqrt{10}-1}{3}$,
所以,能使△ABC为等腰三角形的a的值有4个.
解法2:易得抛物线一定过两个定点:(-1,0),(0,-3),连接这两个定点,得到一条线段,以这条线段为底边可以在横轴上找一点构成等腰三角形,以这条线段为腰,分别以两个定点为顶点可以在横轴上找到三个点构成等腰三角形,所以共有四个点可以与定点构成等腰三角形,从而可以确定四个形状不同的抛物线,所以a有四个值.
故选C.
点评 本题考查了抛物线与x轴的交点问题,根据抛物线的解析式确定出抛物线经过的两个定点是解题的关键,注意分情况讨论,此题有一定的难度.

 53天天练系列答案
53天天练系列答案| A. | 1 | B. | 10 | C. | 18 | D. | 0 |
| A. | 240元 | B. | 280元 | C. | 320元 | D. | 360元 |
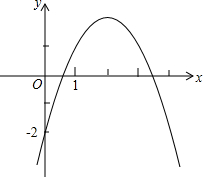 函数y=ax2+bx+c图象如图,根据图象小明做如下判断:①a<0,b>0,c>0同时成立;②函数值y≤$\frac{4ac-{b}^{2}}{4a}$;③当x$<-\frac{b}{2a}$时,y随x的增大而减小;④a+b+c>0,a-b+c<0,b2-4ac>0同时成立.判断正确的个数为( )个.
函数y=ax2+bx+c图象如图,根据图象小明做如下判断:①a<0,b>0,c>0同时成立;②函数值y≤$\frac{4ac-{b}^{2}}{4a}$;③当x$<-\frac{b}{2a}$时,y随x的增大而减小;④a+b+c>0,a-b+c<0,b2-4ac>0同时成立.判断正确的个数为( )个.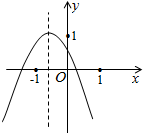 如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,胡娇同学观察得出了下面四条信息:(1)(a≠0)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的信息有( )
如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,胡娇同学观察得出了下面四条信息:(1)(a≠0)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的信息有( )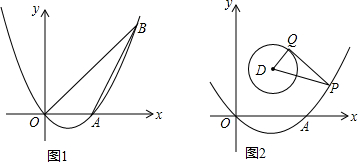
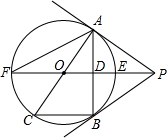 如图,PB为⊙O的切线,B为切点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
如图,PB为⊙O的切线,B为切点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.