题目内容
3. 如图,∠DEB=∠ACB=Rt∠,DE=2,AB=5,BC=3,BD=2.5,求证:AB平分∠DBC.
如图,∠DEB=∠ACB=Rt∠,DE=2,AB=5,BC=3,BD=2.5,求证:AB平分∠DBC.
分析 根据勾股定理得到AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4,由已知条件得到$\frac{DE}{AC}=\frac{BD}{AB}$,证得△DBE∽△ABC,根据相似三角形的性质得到∠DBE=∠ABC,于是得到结论.
解答 证明:∵∠ACB=90°,AB=5,BC=3,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4,
∵$\frac{DE}{AC}=\frac{2}{4}$=$\frac{1}{2}$,$\frac{BD}{AB}$=$\frac{2.5}{5}$=$\frac{1}{2}$,
∴$\frac{DE}{AC}=\frac{BD}{AB}$,
∵∠DEB=∠ACB=90°,
∴△DBE∽△ABC,
∴∠DBE=∠ABC,
∴AB平分∠DBC.
点评 本题考查了相似三角形的判定和性质,勾股定理,角平分线的判定,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.对于下列各式,其中错误的是( )
| A. | (-1)2007=-1 | B. | -(-1)2008=-1 | C. | (-3)2=6 | D. | -(-2)3=8 |
18. 如图,在4×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )
如图,在4×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )
 如图,在4×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )
如图,在4×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
15.A、B两地相距30千米,甲从A地出发以每小时5千米的速度向目的地B行走,则甲与B地间的距离s(千米)与甲行走的时间t(小时)间的函数关系是( )
| A. | s=5t(t≥0) | B. | s=5t(0≤t≤6) | C. | s=30+5t(0≤t≤6) | D. | s=30-5t(0≤t≤6) |
10.下列图案中,既是中心对称图形,又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
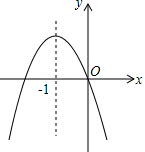 二次函数y=ax2+bx+c的图象如图所示,下列结论:①a+b+c>0;②a-b+c>0;③abc<0;④2a-b=0,其中正确的个数是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论:①a+b+c>0;②a-b+c>0;③abc<0;④2a-b=0,其中正确的个数是( )