题目内容
11.已知在△ABC中,CA=CB,点O在高CH上,OD⊥AC于D,以O为圆心,OD为半径作⊙O.(1)如图①,求证:CB是⊙O的切线;
(2)如图②,若⊙O是△ABC的内切圆,AC=5,AB=6,求⊙O的面积.
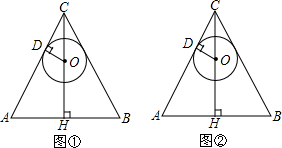
分析 (1)作OE⊥BC于E,由等腰三角形的三线合一性质得出∠ACH=∠BCH,由角平分线的性质得出OE=OD,即可得出结论;
(2)由等腰三角形的三线合一性质得出AH=BH=$\frac{1}{2}$AB,由勾股定理求出CH,再证明△COD∽△CAH,得出对应边成比例,求出OD,即可求出⊙O的面积.
解答 (1)证明:作OE⊥BC于E,如图1所示:
∵CA=CB,点O在高CH上,
∴∠ACH=∠BCH,
∵OD⊥CA,OE⊥CB,
∴OE=OD,
∴CB是⊙O的切线;
(2)解:如图2所示:
∵⊙O是△ABC的内切圆, ∴OH=OD,
∴OH=OD,
∵CA=CB,CH是高,
∴AH=BH=$\frac{1}{2}$AB=3,
∴CH=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵∠OCD=∠ACH,∠CDO=∠CHA=90°,
∴△COD∽△CAH,
∴$\frac{OD}{AH}=\frac{OC}{AC}$,
即$\frac{OD}{3}=\frac{4-OD}{5}$,
解得OD=$\frac{3}{2}$,
∴⊙O的面积=π×($\frac{3}{2}$)2=$\frac{9}{4}π$.
点评 本题考查了切线的判定方法、勾股定理、相似三角形的判定与性质、圆的面积的计算;熟练掌握切线的判定方法,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
相关题目
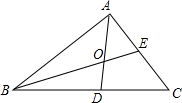 如图,在△ABC中,DC:BC=1:3,BO:OE=4:1,那么CE:EA=1.
如图,在△ABC中,DC:BC=1:3,BO:OE=4:1,那么CE:EA=1. 如题,OA、OB是⊙O的半径,OA⊥OB,⊙O过点C的切线交OB的延长线于点D,E为OD延长线与AC延长线的交点,求证:DC=DE.
如题,OA、OB是⊙O的半径,OA⊥OB,⊙O过点C的切线交OB的延长线于点D,E为OD延长线与AC延长线的交点,求证:DC=DE. 如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC为斜边AC为直角边,画第2个等腰直角三角形ACD,再以Rt△ACD的斜边AD为直角边,画第3个等腰直角三角形ADE…,以此类推,则第15个等腰直角三角形的斜边长为128$\sqrt{2}$.
如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC为斜边AC为直角边,画第2个等腰直角三角形ACD,再以Rt△ACD的斜边AD为直角边,画第3个等腰直角三角形ADE…,以此类推,则第15个等腰直角三角形的斜边长为128$\sqrt{2}$.