题目内容
4. 如图,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$的图象上,第二象限的点B在反比例函数y=$\frac{k}{x}$的图象上,且OA⊥OB,tanA=$\sqrt{2}$,则k的值为( )
如图,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$的图象上,第二象限的点B在反比例函数y=$\frac{k}{x}$的图象上,且OA⊥OB,tanA=$\sqrt{2}$,则k的值为( )| A. | -3 | B. | -4 | C. | -6 | D. | -2$\sqrt{3}$ |
分析 作BC⊥x轴于C,AD⊥x轴于D,如图,利用反比例函数系数的机会意义得到S△AOD=1,再根据正切的意义得到tanA=$\frac{OB}{OA}$=$\sqrt{2}$,则OB=$\sqrt{2}$OA,接着证明Rt△AOD∽Rt△OBC,利用相似三角形的性质得S△OBC=2S△AOD=2,所以$\frac{1}{2}$•|k|=2,然后根据反比例函数的性质确定k的值.
解答 解: 作BC⊥x轴于C,AD⊥x轴于D,如图,则S△AOD=$\frac{1}{2}$×2=1,
作BC⊥x轴于C,AD⊥x轴于D,如图,则S△AOD=$\frac{1}{2}$×2=1,
在Rt△AOB中,tanA=$\frac{OB}{OA}$=$\sqrt{2}$,
∴OB=2OA,
∵∠AOD+∠BOC=90°,∠AOD+∠OAD=90°,
∴∠BOC=∠OAD,
∴Rt△AOD∽Rt△OBC,
∴$\frac{{S}_{△AOD}}{{S}_{△OBC}}$=($\frac{OA}{OB}$)2=2,
∴S△OBC=2S△AOD=2,
∴$\frac{1}{2}$•|k|=2,
而k<0,
∴k=-4.
故选B.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了相似三角形的判定与性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14. 如图,矩形ABCD的两条对角线相交于点O,∠AOB=120°,AD=2,点E是BC的中点,连结OE,则OE的长是( )
如图,矩形ABCD的两条对角线相交于点O,∠AOB=120°,AD=2,点E是BC的中点,连结OE,则OE的长是( )
 如图,矩形ABCD的两条对角线相交于点O,∠AOB=120°,AD=2,点E是BC的中点,连结OE,则OE的长是( )
如图,矩形ABCD的两条对角线相交于点O,∠AOB=120°,AD=2,点E是BC的中点,连结OE,则OE的长是( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 4 |
15.计算$\frac{1}{3}$-$\frac{1}{2}$的结果是( )
| A. | 6的倒数 | B. | 6的相反数 | C. | -6的绝对值 | D. | -6的倒数 |
12.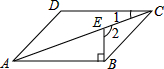 如图,在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=18°,则∠2=( )
如图,在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=18°,则∠2=( )
 如图,在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=18°,则∠2=( )
如图,在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=18°,则∠2=( )| A. | 98° | B. | 102° | C. | 108° | D. | 118° |
19.-$\frac{1}{3}$的倒数是( )
| A. | $\frac{1}{3}$ | B. | -3 | C. | 3 | D. | -$\frac{1}{3}$ |
16.下列调查中最适合采用普查的是( )
| A. | 调查某批次汽车的抗撞击能力 | |
| B. | 调查某班40名同学的视力情况 | |
| C. | 端午节期间,抚顺市食品安全检查部门调查市场上粽子的质量情况 | |
| D. | 调查某池塘中现有雨的数量 |
13. 如图是一个正方体展开图,把展开图折叠成正方体后,“美”字一面相对面上的字是( )
如图是一个正方体展开图,把展开图折叠成正方体后,“美”字一面相对面上的字是( )
 如图是一个正方体展开图,把展开图折叠成正方体后,“美”字一面相对面上的字是( )
如图是一个正方体展开图,把展开图折叠成正方体后,“美”字一面相对面上的字是( )| A. | 云 | B. | 龙 | C. | 湖 | D. | 丽 |
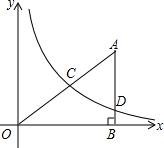 如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直于x轴,垂足为点B,反比例函数y=$\frac{k}{x}$(x>0)的图象经过AO上的点C,且$\frac{OC}{OA}=\frac{2}{3}$,与AB相交于点D,OB=6,AD=$\frac{5}{2}$,
如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直于x轴,垂足为点B,反比例函数y=$\frac{k}{x}$(x>0)的图象经过AO上的点C,且$\frac{OC}{OA}=\frac{2}{3}$,与AB相交于点D,OB=6,AD=$\frac{5}{2}$,