题目内容
△ABC的三边长分a,b,c,且满足c2=4a2,b2=3a2,则△ABC是
直角
直角
三角形.分析:由于c2=4a2,b2=3a2,两式相减可得,c2-b2=a2,利用勾股定理的逆定理,从而确定三角形的形状.
解答:解:∵c2=4a2,b2=3a2,
∴c2-b2=a2,即c2=b2+a2,
∴△ABC是直角三角形.
故答案为:直角.
∴c2-b2=a2,即c2=b2+a2,
∴△ABC是直角三角形.
故答案为:直角.
点评:本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
已知△ABC的三边长分别是6cm、8cm、10cm,则△ABC的面积是( )
| A、24cm2 | B、30cm2 | C、40cm2 | D、48cm2 |
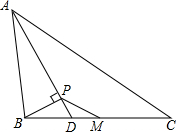 如图,△ABC的三边长分别是AB=14,BC=16,AC=26,P为∠A的平分线AD上一点,且BP⊥AD,M为BC的中点,求PM的长.
如图,△ABC的三边长分别是AB=14,BC=16,AC=26,P为∠A的平分线AD上一点,且BP⊥AD,M为BC的中点,求PM的长.