题目内容
7.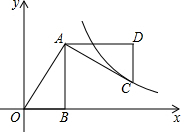 如图,平面直角坐标中,OB在x轴上,∠ABO=90°,点A的坐标为(2,4),将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(x>0)上,则k的值为( )
如图,平面直角坐标中,OB在x轴上,∠ABO=90°,点A的坐标为(2,4),将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(x>0)上,则k的值为( )| A. | 12 | B. | 10 | C. | 8 | D. | 6 |
分析 由A(2,4)可知B0=2,AB=4,由旋转的性质可知AD=AB=4,CD=BO=2,△OAB旋转90°,可知AD∥x轴,CD⊥x轴,根据线段的长度求C点坐标,再求k的值.
解答 解:∵点A的坐标为(2,4).Rt△AOB绕点A逆时针旋转90°,
∴OB+AD=6,AB-CD=2,故C(6,2),
将C(6,2)代入y=$\frac{k}{x}$(x>0)中,得k=6×2=12.
故选:A.
点评 本题考查了反比例函数关系式的求法,旋转的性质.关键是通过旋转确定双曲线上点的坐标.

练习册系列答案
相关题目
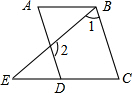 如图,已知∠A=∠C,∠1与∠2互补,
如图,已知∠A=∠C,∠1与∠2互补,