题目内容
12.如果一个矩形较短的边长为5cm.两条对角线所夹的角为60°,则这个矩形的面积是25$\sqrt{3}$cm2.分析 根据矩形对角线相等且互相平分性质和题中条件易得△AOB为等边三角形,即可得到矩形对角线一半长,进而求解即可.
解答 解:如图:AB=5cm,∠AOB=60°,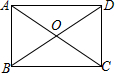
∵四边形是矩形,AC,BD是对角线,
∴OA=OB=OD=OC=$\frac{1}{2}$BD=$\frac{1}{2}$AC,
在△AOB中,OA=OB,∠AOB=60°,
∴OA=OB=AB=5cm,BD=2OB=2×5=10cm,
∴BC=$\sqrt{1{0}^{2}-{5}^{2}}=5\sqrt{3}$cm,
∴矩形的面积=25$\sqrt{3}$cm2.
故答案为:$25\sqrt{3}$.
点评 此题考查矩形的性质,矩形的两对角线所夹的角为60°,那么对角线的一边和两条对角线的一半组成等边三角形.本题比较简单,根据矩形的性质解答即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列几何体的俯视图是三角形的是( )
| A. |  | B. |  | C. |  | D. |  |
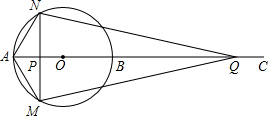 如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以lcm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为l,设运动时间为t秒.
如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以lcm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为l,设运动时间为t秒.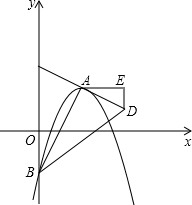 如图,在平面直角坐标系xOy中,抛物线y=-$\frac{1}{4}$(x-m)2+$\frac{1}{4}$m2-m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
如图,在平面直角坐标系xOy中,抛物线y=-$\frac{1}{4}$(x-m)2+$\frac{1}{4}$m2-m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.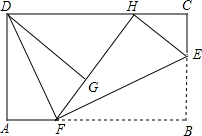 如图,已知长方形的每个角都是直角,将长方形ABCD沿EF折叠后点B
如图,已知长方形的每个角都是直角,将长方形ABCD沿EF折叠后点B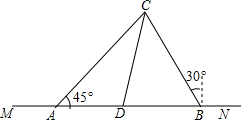 小明与小红分别住在东西大街相距10(1+$\sqrt{3}$)km的点A与点B处.在小明家北偏东45°与小红家北偏西30°的方向有两条公路交于点C,在点C的南偏西15°的方向上,且在点A与点B之间有一个以点D为圆心的方圆5km的大型批发市场.
小明与小红分别住在东西大街相距10(1+$\sqrt{3}$)km的点A与点B处.在小明家北偏东45°与小红家北偏西30°的方向有两条公路交于点C,在点C的南偏西15°的方向上,且在点A与点B之间有一个以点D为圆心的方圆5km的大型批发市场.