题目内容
18．
如图，已知：OA：OA′=OB：OB′=OC：OC′=2：3，求证：△ABC∽△A′B′C′．
分析 先根据两组对应边的比相等且夹角对应相等的两个三角形相似，判断△AOB∽△A′OB′得到$\frac{AB}{A′B′}$=$\frac{2}{3}$，同理可得$\frac{BC}{B′C′}$=$\frac{2}{3}$，$\frac{AC}{A′C′}$=$\frac{2}{3}$，所以$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$=$\frac{AC}{A′C′}$，然后根据三组对应边的比相等的两个三角形相似即可得到结论．
解答 证明：∵OA：OA′=OB：OB′，
而∠AOB=∠A′OB′，
∴△AOB∽△A′OB′，
∴$\frac{AB}{A′B′}$=$\frac{OA}{OA′}$=$\frac{2}{3}$，
同理可得△COB∽△C′OB′，△AOC∽△A′OC′，
∴$\frac{BC}{B′C′}$=$\frac{OC}{OC′}$=$\frac{2}{3}$，$\frac{AC}{A′C′}$=$\frac{2}{3}$，
∴$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$=$\frac{AC}{A′C′}$，
∴△ABC∽△A′B′C′．
点评 本题考查了相似三角形的判定：两组对应边的比相等且夹角对应相等的两个三角形相似；三组对应边的比相等的两个三角形相似．也考查了相似三角形的性质．
练习册系列答案
相关题目
3．大圆的半径为acm，小圆的半径比大圆的半径小1cm，则两圆的面积和为（ ）cm2．
| A． | πa2 | B． | π（a-1）2 | C． | πa2+π（a-1）2 | D． | a2+（a-1）2 |
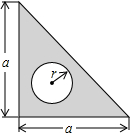一块三角尺的形状和尺寸如图所示，如果圆孔的半径是r，三角尺的厚度是h，用式子表示这块三角尺的体积V，若a=6cm，r=0.5cm，h=0.2cm，求V的值（π取3）．
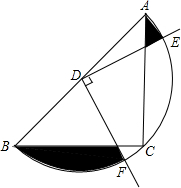如图，在△ABC中，CA=CB，∠ACB=90°，AB=4，点D为AB的中点，以点D为圆心作圆，半圆恰好经过三角形的直角顶点C，以点D为顶点，作90°的∠EDF，与半圆交于点E，F，则图中阴影部分的面积是π-2．