题目内容
如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、A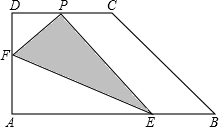 D上,将△AEF沿EF翻折,点A的落点记为P.
D上,将△AEF沿EF翻折,点A的落点记为P.(1)当AE=5,P落在线段CD上时,PD=
(2)当P落在直角梯形ABCD内部时,PD的最小值等于
分析:(1)过P作PG⊥AB于G,则四边形DAGP是矩形,由折叠的性质知PE=AE=5,由勾股定理得出相关的线段的长度,即可求得DP的长;
(2)当点P落在梯形的内部时,∠P=∠A=90°,四边形PFAE是以EF为直径的圆内接四边形,只有当直径EF最大时,且点A落在BD上时,PD最小,此时E与点B重合,由勾股定理得BD的长,从而求得PD=4
-8.
(2)当点P落在梯形的内部时,∠P=∠A=90°,四边形PFAE是以EF为直径的圆内接四边形,只有当直径EF最大时,且点A落在BD上时,PD最小,此时E与点B重合,由勾股定理得BD的长,从而求得PD=4
| 5 |
解答: 解:(1)过P作PG⊥AB于G,则四边形DAGP是矩形,PG=DA=4,
解:(1)过P作PG⊥AB于G,则四边形DAGP是矩形,PG=DA=4,
∵PE=AE=5,
∴GE=
=
=3,
∴PD=AG=AE-GE=5-3=2;
(2)连接ED,作P1P⊥ED于P,
那么在Rt△P1PD中,P1D>PD,
故当点A的对称点P落在线段ED上时,PD有最小值,(左图)
而E在线段AB上,
故当E与B重合时,即EP=BP,此时PD取最小值.(右图)
此时,AB=BP=8,又BD=
=4
,
∴PD=BD-BP=4
-8.

 解:(1)过P作PG⊥AB于G,则四边形DAGP是矩形,PG=DA=4,
解:(1)过P作PG⊥AB于G,则四边形DAGP是矩形,PG=DA=4,∵PE=AE=5,
∴GE=
| PE2-PG2 |
| 52-42 |
∴PD=AG=AE-GE=5-3=2;
(2)连接ED,作P1P⊥ED于P,
那么在Rt△P1PD中,P1D>PD,
故当点A的对称点P落在线段ED上时,PD有最小值,(左图)
而E在线段AB上,
故当E与B重合时,即EP=BP,此时PD取最小值.(右图)
此时,AB=BP=8,又BD=
| AB2+AD2 |
| 5 |
∴PD=BD-BP=4
| 5 |

点评:本题利用了:1、折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;2、矩形的性质,直角三角形的性质,勾股定理求解.

练习册系列答案
相关题目
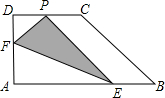 如图,直角梯形纸片ABCD,AD⊥AB,AB=6,AD=CD=3,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.当P落在直角梯形ABCD内部时,PD的最小值等于
如图,直角梯形纸片ABCD,AD⊥AB,AB=6,AD=CD=3,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.当P落在直角梯形ABCD内部时,PD的最小值等于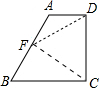 如图,直角梯形纸片ABCD中,∠DCB=90°,AD∥BC,将纸片折叠,使顶点B与顶点D重合,折痕为CF.
如图,直角梯形纸片ABCD中,∠DCB=90°,AD∥BC,将纸片折叠,使顶点B与顶点D重合,折痕为CF. (2013•临汾二模)如图,直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°.折叠纸片使BC经过点D,点C落在点E处,BF是折痕,且BF=CF=8.则AB的长是
(2013•临汾二模)如图,直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°.折叠纸片使BC经过点D,点C落在点E处,BF是折痕,且BF=CF=8.则AB的长是 (2012•内江模拟)如图,直角梯形纸片ABCD,AD⊥AB,AD=CD=4,点E、F分别在线段AB、CD上,将△AEF沿EF翻折,点A落在线段CD上的点P处,若AE=5,则PF的长为( )
(2012•内江模拟)如图,直角梯形纸片ABCD,AD⊥AB,AD=CD=4,点E、F分别在线段AB、CD上,将△AEF沿EF翻折,点A落在线段CD上的点P处,若AE=5,则PF的长为( )