题目内容
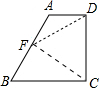 如图,直角梯形纸片ABCD中,∠DCB=90°,AD∥BC,将纸片折叠,使顶点B与顶点D重合,折痕为CF.
如图,直角梯形纸片ABCD中,∠DCB=90°,AD∥BC,将纸片折叠,使顶点B与顶点D重合,折痕为CF.若AD=2,BC=5,则AF:FB的值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:根据题意延长CF交DA延长线于E,然后根据折叠的性质得出DC=BC,CF是∠BCD的平分线,∠DCE=45°,即△EDC是等腰直角三角形,再由AD∥BC求解.
解答: 解:延长CF交DA于E,
解:延长CF交DA于E,
将纸片折叠,使顶点B与顶点D重合,则DC=BC,CF是∠BCD的平分线,∠DCE=45°,
∴△EDC是等腰直角三角形,DE=DC=5,AE=5-2=3,BC=5,
∵AD∥BC,
∴∠E=∠FCB,∠EAF=∠B,
∴△AEF∽△BCF,
∴AF:FB=AE:BC=
,
故选D.
 解:延长CF交DA于E,
解:延长CF交DA于E,将纸片折叠,使顶点B与顶点D重合,则DC=BC,CF是∠BCD的平分线,∠DCE=45°,
∴△EDC是等腰直角三角形,DE=DC=5,AE=5-2=3,BC=5,
∵AD∥BC,
∴∠E=∠FCB,∠EAF=∠B,
∴△AEF∽△BCF,
∴AF:FB=AE:BC=
| 3 |
| 5 |
故选D.
点评:本题主要考查了:①折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等,②直角梯形的性质和平行的比例关系求解,难度适中.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
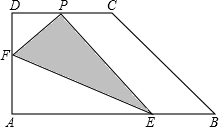 D上,将△AEF沿EF翻折,点A的落点记为P.
D上,将△AEF沿EF翻折,点A的落点记为P.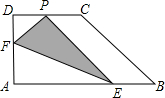 如图,直角梯形纸片ABCD,AD⊥AB,AB=6,AD=CD=3,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.当P落在直角梯形ABCD内部时,PD的最小值等于
如图,直角梯形纸片ABCD,AD⊥AB,AB=6,AD=CD=3,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.当P落在直角梯形ABCD内部时,PD的最小值等于 (2013•临汾二模)如图,直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°.折叠纸片使BC经过点D,点C落在点E处,BF是折痕,且BF=CF=8.则AB的长是
(2013•临汾二模)如图,直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°.折叠纸片使BC经过点D,点C落在点E处,BF是折痕,且BF=CF=8.则AB的长是 (2012•内江模拟)如图,直角梯形纸片ABCD,AD⊥AB,AD=CD=4,点E、F分别在线段AB、CD上,将△AEF沿EF翻折,点A落在线段CD上的点P处,若AE=5,则PF的长为( )
(2012•内江模拟)如图,直角梯形纸片ABCD,AD⊥AB,AD=CD=4,点E、F分别在线段AB、CD上,将△AEF沿EF翻折,点A落在线段CD上的点P处,若AE=5,则PF的长为( )