题目内容
已知如图,△ABC是⊙O的内接正三角形,弦EF经过BC边的中点D,且EF∥BA,若⊙O的半径为 ,则DE的长为( )
,则DE的长为( )
A.

B.
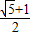
C.
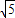 -1
-1D.

【答案】分析:根据等边三角形的性质求得圆的半径,然后根据中位线定理求得DG的长,利用勾股定理求得EG,即可求得EF的长,根据ED= 即可求解.
即可求解.
解答: 解:连接OC交EF于M,延长CM交AB于点H.连接OA,连接OE.
解:连接OC交EF于M,延长CM交AB于点H.连接OA,连接OE.
在直角△OAH中,AH=OA•cos30°=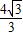 ×
×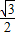 =2
=2
∴AB=2AH=4
又∵弦EF经过BC边的中点D,且EF∥BA.
∴DG= AB=2,
AB=2,
在直角△ACH中,CH=AC•sin60°=4×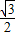 =2
=2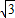 ,
,
∴OH= CH=
CH= ,
,
HM= CH=
CH= ,
,
∴OM=HM-OH=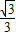 ,
,
在直角△OME中,EM=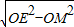 =
=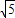 ,
,
∴EF=2 ,
,
∴ED=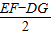 =
= -1.
-1.
故选C.
点评:本题主要考查了勾股定理以及垂径定理,三角形的中位线定理,利用垂径定理正确求得EF的长是解题的关键.
 即可求解.
即可求解.解答:
 解:连接OC交EF于M,延长CM交AB于点H.连接OA,连接OE.
解:连接OC交EF于M,延长CM交AB于点H.连接OA,连接OE.在直角△OAH中,AH=OA•cos30°=
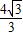 ×
×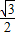 =2
=2∴AB=2AH=4
又∵弦EF经过BC边的中点D,且EF∥BA.
∴DG=
 AB=2,
AB=2,在直角△ACH中,CH=AC•sin60°=4×
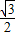 =2
=2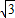 ,
,∴OH=
 CH=
CH= ,
,HM=
 CH=
CH= ,
,∴OM=HM-OH=
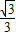 ,
,在直角△OME中,EM=
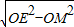 =
=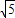 ,
,∴EF=2
 ,
,∴ED=
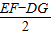 =
= -1.
-1.故选C.
点评:本题主要考查了勾股定理以及垂径定理,三角形的中位线定理,利用垂径定理正确求得EF的长是解题的关键.

练习册系列答案
相关题目
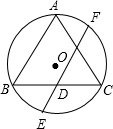 已知如图,△ABC是⊙O的内接正三角形,弦EF经过BC边的中点D,且EF∥BA,若⊙O的半径为
已知如图,△ABC是⊙O的内接正三角形,弦EF经过BC边的中点D,且EF∥BA,若⊙O的半径为4
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|

 22、已知如图,△ABC是等腰直角三角形,∠C为直角.
22、已知如图,△ABC是等腰直角三角形,∠C为直角. 已知如图,△ABC是等边三角形,E、G是AB边的三等分点,F、H是AC边的三等分点,则图中阴影部分的面积是△ABC的面积的( )
已知如图,△ABC是等边三角形,E、G是AB边的三等分点,F、H是AC边的三等分点,则图中阴影部分的面积是△ABC的面积的( ) 已知如图,△ABC是等边三角形,P是三角形外的一点,且∠ABP+∠ACP=180°.
已知如图,△ABC是等边三角形,P是三角形外的一点,且∠ABP+∠ACP=180°.