题目内容
3.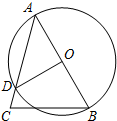 如图,在△ABC中,AB是⊙O的直径,⊙O与AC交于点D,AC=$\sqrt{6}$,∠B=60°,∠C=75°.
如图,在△ABC中,AB是⊙O的直径,⊙O与AC交于点D,AC=$\sqrt{6}$,∠B=60°,∠C=75°.(1)求∠BOD的度数;
(2)求BC的长.
分析 (1)先根据三角形内角和定理求出∠A的度数,再由圆周角定理即可得出结论;
(2)过点C作CE⊥AB于点E,先根据锐角三角函数的定义求出CE的长,同理可得出BC的长.
解答 解:(1)∵∠B=60°,∠C=75°,
∴在△ABC中,∠A=180°-∠ABC-∠C=45°,
∴∠BOD=2∠A=90°;
(2)过点C作CE⊥AB于点E,在Rt△ACE中,CE=$\frac{\sqrt{2}}{2}$AC=$\sqrt{3}$,
在Rt△BCE中,
∵∠ABC=60°,
∴BC=$\frac{2}{\sqrt{3}}$BE=2.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
11.适合下列条件的△ABC中,是直角三角形的个数为( )
①a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$②∠A-∠B=∠C③∠A=32°,∠B=58°④a=7,b=24,c=25.
①a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$②∠A-∠B=∠C③∠A=32°,∠B=58°④a=7,b=24,c=25.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.对于实数c,d,我们可用min{c,d}表示c,d两数中较小的数,如min{3,-1}=-1.则关于x的代数式min{3x${\;}^{2}-\frac{3}{2}$,x2+2x+1}的最小值是( )
| A. | $\frac{3}{2}$ | B. | -1 | C. | -$\frac{3}{2}$ | D. | -2 |
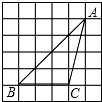 在正方形网格中,△ABC如图所示放置在网格中,则tanA=$\frac{3}{5}$.
在正方形网格中,△ABC如图所示放置在网格中,则tanA=$\frac{3}{5}$.