题目内容
设实数a,b,c,m满足条件
+
+
=0,且a≥0,m>0,求证:方程ax2+bx+c=0有一根x0,满足0<x0<1.
| a |
| m+2 |
| b |
| m+1 |
| c |
| m |
考点:一元二次方程根的分布
专题:证明题
分析:利用当c=0以及c>0和c<0,分别将已知变形得出 f(x)有一个根x=
在(0,1)间,进而得出答案.
| m+1 |
| m+2 |
解答:解:设f(x)=ax2+bx+c,
如果c=0,那么
+
+
=0,则
+
=0,
故
+b=0,
即f(
)=0.
f(x)有一个根x=
在(0,1)间.
如果c>0,
∵
+
+
=0
∴
+
+c=0
故
+c=
,
则f(
)=
+
+c
=
+
=am(
-
)
=am×
=-
≤0,
所以f(0)>0,f(
)≤0.故f(x)必有一根在0和
之间,
即方程ax2+bx+c=0有一根x0,满足0<x0<1;
若c<0,f(1)=a+b+c=a+(m+1)[-
-
]+c=
-
>0,
故方程f(x)=0在(
,1)内有解.
综上所述:方程ax2+bx+c=0有一根x0,满足0<x0<1.
如果c=0,那么
| a |
| m+2 |
| b |
| m+1 |
| c |
| m |
| a |
| m+2 |
| b |
| m+1 |
故
| a(m+1) |
| m+2 |
即f(
| m+1 |
| m+2 |
f(x)有一个根x=
| m+1 |
| m+2 |
如果c>0,
∵
| a |
| m+2 |
| b |
| m+1 |
| c |
| m |
∴
| am |
| m+2 |
| bm |
| m+1 |
故
| bm |
| m+1 |
| -am |
| m+2 |
则f(
| m |
| m+1 |
| am2 |
| (m+1)2 |
| bm |
| m+1 |
=
| am2 |
| (m+1)2 |
| -am |
| m+2 |
=am(
| m |
| (m+1)2 |
| 1 |
| m+2 |
=am×
| m(m+2)-(m+1)2 |
| (m+2)(m+1)2 |
=-
| am |
| (m+2)(m+1)2 |
所以f(0)>0,f(
| m |
| m+1 |
| m |
| m+1 |
即方程ax2+bx+c=0有一根x0,满足0<x0<1;
若c<0,f(1)=a+b+c=a+(m+1)[-
| c |
| m |
| a |
| m+2 |
| a |
| m+2 |
| c |
| m |
故方程f(x)=0在(
| m |
| m+1 |
综上所述:方程ax2+bx+c=0有一根x0,满足0<x0<1.
点评:此题主要考查了一元二次方程根的分布,正确分类讨论得出是解题关键.

练习册系列答案
相关题目
下列说法错误的是( )
| A、直径是圆中最长的弦 |
| B、长度相等的两条弧是等弧 |
| C、面积相等的两个圆是等圆 |
| D、半径相等的两个半圆是等弧 |
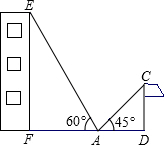 如图,在一次课外数学实践活动中,小明站在操场的A处,他的两侧分别是旗杆CD和一幢教学楼EF,点A、D、F在同一直线上,从A处测得旗杆顶部和教学楼顶部的仰角分别为45°和60°,已知DF=16m,EF=18m,求旗杆CD高.(结果精确到0.1m,参考数据:
如图,在一次课外数学实践活动中,小明站在操场的A处,他的两侧分别是旗杆CD和一幢教学楼EF,点A、D、F在同一直线上,从A处测得旗杆顶部和教学楼顶部的仰角分别为45°和60°,已知DF=16m,EF=18m,求旗杆CD高.(结果精确到0.1m,参考数据: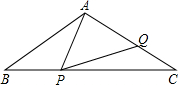 如图,在等腰△ABC中,AB=AC=6cm,BC=10cm,点P从点B出发,以2cm/s的速度沿BC向点C运动,设点P的运动时间为t s.
如图,在等腰△ABC中,AB=AC=6cm,BC=10cm,点P从点B出发,以2cm/s的速度沿BC向点C运动,设点P的运动时间为t s.