题目内容
 如图,抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,-3)
如图,抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,-3)(1)求抛物线的解析式;
(2)在x轴下方的抛物线上是否存在在一点D,使四边形ABCD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由;
(3)在抛物线y=ax2+bx+c上求点E,使△BCE是以BC为直角边的直角三角形.
考点:二次函数综合题
专题:
分析:(1)把点A、B、C的坐标分别代入函数解析式列出关于a、b、c的方程组,通过解方程组可以求得它们的值;
(2)设D(m,m2-2m-3),连接OD,把四边形ABDC的面积分成△AOC,△DOC,△DOB的面积和,求表达式的最大值;
(3)有两种可能:B为直角顶点;C为直角顶点;要充分认识△OBC的特殊性,是等腰直角三角形,可以通过解直角三角形求出相关线段的长度.
(2)设D(m,m2-2m-3),连接OD,把四边形ABDC的面积分成△AOC,△DOC,△DOB的面积和,求表达式的最大值;
(3)有两种可能:B为直角顶点;C为直角顶点;要充分认识△OBC的特殊性,是等腰直角三角形,可以通过解直角三角形求出相关线段的长度.
解答: 解:(1)∵抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),
解:(1)∵抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),
∴
,
解得
.
则该抛物线的解析式为:y=x2-2x-3;
(2)如图,设D(m,m2-2m-3),连接OD.
则0<m<3,m2-2m-3<
且△AOC的面积=
,△DOC的面积=
m,
△DOB的面积=-
(m2-2m-3),
∴S四边形ABDC=S△AOC+S△DOC+S△DOB
=-
m2+
m+6
=-
(m-
)2+
.
∴存在点D(
,-
),使四边形ABDC的面积最大为
;
(3)有两种情况:
 如图(2),过点B作BE1⊥BC,交抛物线于点E1、交y轴于点F,连接E1C.
如图(2),过点B作BE1⊥BC,交抛物线于点E1、交y轴于点F,连接E1C.
∵∠CBO=45°,
∴∠FBO=45°,BO=OF=3.
∴点F的坐标为(0,3).
∴直线BF的解析式为y=-x+3.
则
,
解得
,
,
∴点E1的坐标为(-2,5).
 如图(3),过点C作CG⊥CB,交抛物线于点E2、交x轴于点G,连接BE2.
如图(3),过点C作CG⊥CB,交抛物线于点E2、交x轴于点G,连接BE2.
∵∠CBO=45°,
∴∠CGB=45°,OG=OC=3.
∴点G的坐标为(-3,0).
∴直线CG的解析式为y=-x-3.
由
,
解得
,
,
∴点E2的坐标为(1,-4).
综上,在抛物线上存在点E1(-2,5)、E2(1,-4),使△BCE1、△BCE2是以BC为直角边的直角三角形.
 解:(1)∵抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),
解:(1)∵抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),∴
|
解得
|
则该抛物线的解析式为:y=x2-2x-3;
(2)如图,设D(m,m2-2m-3),连接OD.
则0<m<3,m2-2m-3<
且△AOC的面积=
| 3 |
| 2 |
| 3 |
| 2 |
△DOB的面积=-
| 3 |
| 2 |
∴S四边形ABDC=S△AOC+S△DOC+S△DOB
=-
| 3 |
| 2 |
| 9 |
| 2 |
=-
| 3 |
| 2 |
| 3 |
| 2 |
| 75 |
| 8 |
∴存在点D(
| 3 |
| 2 |
| 15 |
| 4 |
| 75 |
| 8 |
(3)有两种情况:
 如图(2),过点B作BE1⊥BC,交抛物线于点E1、交y轴于点F,连接E1C.
如图(2),过点B作BE1⊥BC,交抛物线于点E1、交y轴于点F,连接E1C.∵∠CBO=45°,
∴∠FBO=45°,BO=OF=3.
∴点F的坐标为(0,3).
∴直线BF的解析式为y=-x+3.
则
|
解得
|
|
∴点E1的坐标为(-2,5).
 如图(3),过点C作CG⊥CB,交抛物线于点E2、交x轴于点G,连接BE2.
如图(3),过点C作CG⊥CB,交抛物线于点E2、交x轴于点G,连接BE2.∵∠CBO=45°,
∴∠CGB=45°,OG=OC=3.
∴点G的坐标为(-3,0).
∴直线CG的解析式为y=-x-3.
由
|
解得
|
|
∴点E2的坐标为(1,-4).
综上,在抛物线上存在点E1(-2,5)、E2(1,-4),使△BCE1、△BCE2是以BC为直角边的直角三角形.
点评:本题考查了待定系数法求二次函数解析式、二次函数图象上点的坐标特征以及不规则图形面积的求法等二次函数综合题型.解答(2)题时,也可过点M作抛物线的对称轴,将四边形ABMC的面积转化为求一个梯形与两个直角三角形面积的和.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
四个数-5,0,
,
中为无理数的是( )
| 1 |
| 2 |
| 3 |
| A、-5 | ||
| B、0 | ||
C、
| ||
D、
|
 下面左图所示的几何体的俯视图是( )
下面左图所示的几何体的俯视图是( )A、 |
B、 |
C、 |
D、 |
 如图是一些大小相同的小正方体组成的几何体,则其俯视图是( )
如图是一些大小相同的小正方体组成的几何体,则其俯视图是( )A、 |
B、 |
C、 |
D、 |
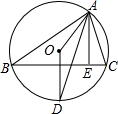 如图,O是△ABC的外心,D是圆上一点,且OD⊥BC,AE是BC边上的高.试探索∠OAD与∠EAD的大小关系,并说明理由.
如图,O是△ABC的外心,D是圆上一点,且OD⊥BC,AE是BC边上的高.试探索∠OAD与∠EAD的大小关系,并说明理由. 已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为
已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为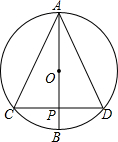 如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是
如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是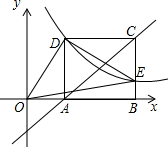 如图,已知正方形ABCD的边长为2,双曲线y=
如图,已知正方形ABCD的边长为2,双曲线y=