题目内容
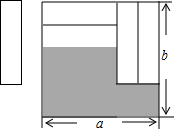 如图,把四张形状大小完全相同的小长方形卡片不重叠地放在一个底面为长方形(长为a,宽为b)的盒子底部,盒子底面未被卡片覆盖的部分用阴影表示,则这两块阴影部分小长方形周长的和为( )
如图,把四张形状大小完全相同的小长方形卡片不重叠地放在一个底面为长方形(长为a,宽为b)的盒子底部,盒子底面未被卡片覆盖的部分用阴影表示,则这两块阴影部分小长方形周长的和为( )| A、a+2b | B、4a |
| C、4b | D、2a+b |
考点:整式的加减
专题:计算题
分析:先设小长方形卡片的长为m,宽为n,再结合图形得出两部分的阴影周长加起来即可求出答案.
解答: 解:设小长方形卡片的长为m,宽为n,
解:设小长方形卡片的长为m,宽为n,
∴L1周长=2(b-2n)+m,
L2周长=2×2n+(b-m),
∴两块阴影部分小长方形周长的和=2(b-2n)+m+2×2n+(b-m)=4b,
故选:C.
 解:设小长方形卡片的长为m,宽为n,
解:设小长方形卡片的长为m,宽为n,∴L1周长=2(b-2n)+m,
L2周长=2×2n+(b-m),
∴两块阴影部分小长方形周长的和=2(b-2n)+m+2×2n+(b-m)=4b,
故选:C.
点评:本题主要考查了整式的加减运算,在解题时要根据题意结合图形得出答案是解题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
下列说法中正确的是( )
| A、-4没有立方根 | ||||
| B、1的立方根是±1 | ||||
C、
| ||||
D、-5的立方根是
|
 如图,直线l1∥l2,则∠α为( )
如图,直线l1∥l2,则∠α为( )| A、40° | B、50° |
| C、60° | D、70° |
某种水果的售价每千克x元,用面值为50元的人民币购买了3千克,应找回( )
| A、50-3x | B、3x |
| C、47x | D、50x-3 |
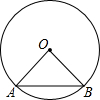 如图,⊙O的半径OA,OB,且OA⊥OB,连结AB.在⊙O上找一点C,使OA2+AB2=BC2,则∠OAC的度数为
如图,⊙O的半径OA,OB,且OA⊥OB,连结AB.在⊙O上找一点C,使OA2+AB2=BC2,则∠OAC的度数为
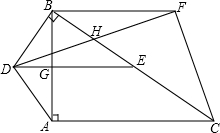 如图,在Rt△ABC中,∠BAC=90°,DB⊥BC,DA=DB,点E是BC的中点,DE与AB相交于点G.
如图,在Rt△ABC中,∠BAC=90°,DB⊥BC,DA=DB,点E是BC的中点,DE与AB相交于点G.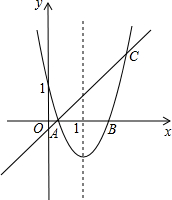 如图,一次函数y=x-
如图,一次函数y=x-