题目内容
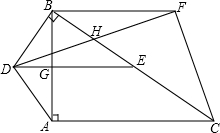 如图,在Rt△ABC中,∠BAC=90°,DB⊥BC,DA=DB,点E是BC的中点,DE与AB相交于点G.
如图,在Rt△ABC中,∠BAC=90°,DB⊥BC,DA=DB,点E是BC的中点,DE与AB相交于点G.(1)求证:DE⊥AB;
(2)如果∠FCB=∠FBC=∠DAB,设DF与BC交于点H,求证:DH=FH.
考点:平行四边形的判定与性质,线段垂直平分线的性质,直角三角形斜边上的中线
专题:证明题
分析:(1)欲证明DE⊥AB,只需推知AE=BE即可;
(2)欲证明DH=FH,需要证得四边形BDEF是平行四边形.
(2)欲证明DH=FH,需要证得四边形BDEF是平行四边形.
解答: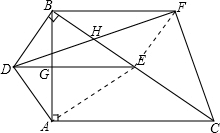 证明:(1)如图,连接AE.
证明:(1)如图,连接AE.
∵∠BAC=90°,BE=EC,
∴AE=BE=
BC.
又∵DA=DB,
∴DE垂直平分AB,即DE⊥AB;
(2)∵∠DBC=90°
∴∠DBA+∠ABC=90°
∵DA=DB,
∴∠DBA=∠DAB,
∵∠FBC=∠DAB
∴∠FBC+∠ABC=90°
∵∠AGE=90°
∴BF∥DE.
又∵∠FBC=∠FCB,
∴FB=FC
∵BE=EC,∴FE⊥BC
∴∠DBE=∠BEF=90°
∴DB∥EF,
∴四边形DBFE是平行四边形,
∴DH=FH.
 证明:(1)如图,连接AE.
证明:(1)如图,连接AE.∵∠BAC=90°,BE=EC,
∴AE=BE=
| 1 |
| 2 |
又∵DA=DB,
∴DE垂直平分AB,即DE⊥AB;
(2)∵∠DBC=90°
∴∠DBA+∠ABC=90°
∵DA=DB,
∴∠DBA=∠DAB,
∵∠FBC=∠DAB
∴∠FBC+∠ABC=90°
∵∠AGE=90°
∴BF∥DE.
又∵∠FBC=∠FCB,
∴FB=FC
∵BE=EC,∴FE⊥BC
∴∠DBE=∠BEF=90°
∴DB∥EF,
∴四边形DBFE是平行四边形,
∴DH=FH.
点评:本题考查了平行四边形的判定与性质,线段垂直平分线的性质以及直角三角形斜边上的中线.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.

练习册系列答案
相关题目
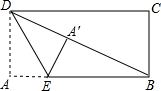 如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为( )
如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为( )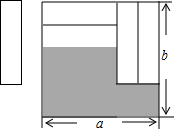 如图,把四张形状大小完全相同的小长方形卡片不重叠地放在一个底面为长方形(长为a,宽为b)的盒子底部,盒子底面未被卡片覆盖的部分用阴影表示,则这两块阴影部分小长方形周长的和为( )
如图,把四张形状大小完全相同的小长方形卡片不重叠地放在一个底面为长方形(长为a,宽为b)的盒子底部,盒子底面未被卡片覆盖的部分用阴影表示,则这两块阴影部分小长方形周长的和为( )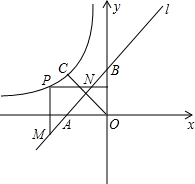 如图,直线l:y=x+2与x轴、y轴分别交于A、B两点,点C与原点O关于直线l对称.反比例函数y=
如图,直线l:y=x+2与x轴、y轴分别交于A、B两点,点C与原点O关于直线l对称.反比例函数y=
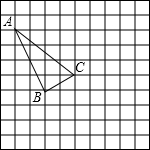 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-2,4),(2,1).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-2,4),(2,1).