题目内容
【题目】已知∠ABC=30°,点D在射线BC上,且到A点的距离等于线段a的长.
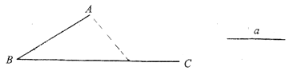
(1)用圆规和直尺在图中作出点D:(不写作法,但须保留作图痕迹,且说明结果
(2)如果AB=8,a=5.求△ABD的面积.
【答案】(1)作图见解析;(2)![]() 和
和![]()
【解析】
(1)以点A为圆心,以线段a的长为半径画弧,交BC于点D.则结论可得;
(2)过A作AE⊥BD于点E,根据30°角所对的直角边等于斜边的一半求出AE的长,再由勾股定理分别求出BE和DE的长,进而求得BD的长,依据三角形面积公式进行计算即可得解.
(1)如图所示:

(2)过A作AE⊥BD于点E,如图1,

∵∠ABE=30°,AB=8,
∴AE=![]() AB=4,
AB=4,
在Rt△ABE中,![]()
在Rt△ADE中,AE=4,AD=5,
∴![]() ,
,
∴BD=BE+DE=![]() ,
,
∴S△ABD=![]() =
=![]() ;
;
如图2,

∵∠ABE=30°,AB=8,
∴AE=![]() AB=4,
AB=4,
在Rt△ABE中,![]()
在Rt△ADE中,AE=4,AD=5,
∴![]() ,
,
∴BD=BE-DE=![]() ,
,
∴S△ABD=![]() =
=![]()

练习册系列答案
相关题目