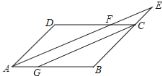
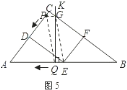
题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点.点
的中点.点![]() 从点
从点![]() 出发沿折线
出发沿折线![]() 以每秒
以每秒![]() 个单位长的速度匀速运动;点
个单位长的速度匀速运动;点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒
方向以每秒![]() 个单位长的速度匀速运动,过点
个单位长的速度匀速运动,过点![]() 作射线
作射线![]() ,交折线
,交折线![]() 于点
于点![]() .点
.点![]() ,
,![]() 同时出发,当点
同时出发,当点![]() 绕行一周回到点
绕行一周回到点![]() 时停止运动,点
时停止运动,点![]() 也随之停止.设点
也随之停止.设点![]() ,
,![]() 运动的时间是
运动的时间是![]() 秒
秒![]() .
.

(1)![]() ,
,![]() 两点间的距离是________;
两点间的距离是________;
![]() 射线
射线![]() 能否把四边形
能否把四边形![]() 分成面积相等的两部分?若能,求出
分成面积相等的两部分?若能,求出![]() 的值;若不能,说明理由;
的值;若不能,说明理由;
![]() 当点
当点![]() 运动到折线
运动到折线![]() 上,且点
上,且点![]() 又恰好落在射线
又恰好落在射线![]() 上时,求
上时,求![]() 的值;
的值;
![]() 连接
连接![]() ,当
,当![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.
【答案】(1)25(2)能(3)![]() 或
或![]() (4)
(4)![]() ;
;![]()
【解析】
(1)由中位线定理即可求出DF的长;
(2)连接DF,过点F作FH⊥AB于点H,由四边形CDEF为矩形,QK把矩形CDEF分为面积相等的两部分,根据△HBF∽△CBA,对应边的比相等,就可以求得t的值;
(3)①当点P在EF上(2![]() ≤t≤5)时根据△PQE∽△BCA,根据相似三角形的对应边的比相等,可以求出t的值;
≤t≤5)时根据△PQE∽△BCA,根据相似三角形的对应边的比相等,可以求出t的值;
②当点P在FC上(5≤t≤7![]() )时,PB=PF+BF就可以得到;
)时,PB=PF+BF就可以得到;
(4)当PG∥AB时四边形PHQG是矩形,由此可以直接写出t.
(1)![]() .
.![]() 能.
能.
如图![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
∵![]() ,
,![]() 是
是![]() ,
,![]() 的中点,
的中点,
∴![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,
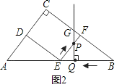
∴![]() 过
过![]() 的中点
的中点![]() 时,即过矩形
时,即过矩形![]() 的中点,
的中点,![]() 把矩形
把矩形![]() 分为面积相等的两部分
分为面积相等的两部分
此时![]() .由
.由![]() ,
,![]() ,得
,得![]() .
.
故![]() .
.![]() ①当点
①当点![]() 在
在![]() 上
上![]() 时,
时,
如图![]() ,
,![]() ,
,![]() ,
,
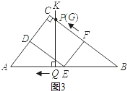
由![]() ,得
,得![]() .
.
∴![]() ;
;
②当点![]() 在
在![]() 上
上![]() 时,
时,
如图![]() ,已知
,已知![]() ,从而
,从而![]() ,
,
由![]() ,
,![]() ,得
,得![]() .
.
解得![]() ;
;
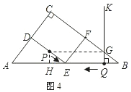
![]() 如图
如图![]() ,
,![]() ;如图
;如图![]() ,
,![]() .
.
(注:判断![]() 可分为以下几种情形:当
可分为以下几种情形:当![]() 时,点
时,点![]() 下行,点
下行,点![]() 上行,可知其中存在
上行,可知其中存在![]() 的时刻,
的时刻,
如图![]() ;此后,点
;此后,点![]() 继续上行到点
继续上行到点![]() 时,
时,![]() ,而点
,而点![]() 却在下行到点
却在下行到点![]() 再沿
再沿![]() 上行,发现点
上行,发现点![]() 在
在![]() 上运动时不存在
上运动时不存在![]() ;
;![]() 当时,点
当时,点![]() ,
,![]() 均在
均在![]() 上,也不存在
上,也不存在![]() ;由于点
;由于点![]() 比点
比点![]() 先到达点
先到达点![]() 并继续沿
并继续沿![]() 下行,所以在
下行,所以在
![]() 中存在
中存在![]() 的时刻,如图
的时刻,如图![]()
![]() 时,点
时,点![]() ,
,![]() 均在
均在![]() 上,不存在
上,不存在![]() .
.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目