题目内容
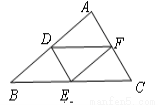
12. 如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到100个小三角形,则需要操作的次数是( )
如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到100个小三角形,则需要操作的次数是( )| A. | 25 | B. | 33 | C. | 34 | D. | 50 |
分析 由第一次操作后三角形共有4个、第二次操作后三角形共有(4+3)个、第三次操作后三角形共有(4+3+3)个,可得第n次操作后三角形共有4+3(n-1)=3n+1个,根据题意得3n+1=100,求得n的值即可.
解答 解:∵第一次操作后,三角形共有4个;
第二次操作后,三角形共有4+3=7个;
第三次操作后,三角形共有4+3+3=10个;
…
∴第n次操作后,三角形共有4+3(n-1)=3n+1个;
当3n+1=100时,解得:n=33,
故选:B.
点评 此题主要考查了图形的变化类,根据已知得出第n次操作后,三角形的个数为3n+1是解题关键.

练习册系列答案
相关题目
2.坐标平面上有一个二元一次方程式的图形,此图形通过(-3,0)、(0,-5)两点.判断此图形与下列哪一个方程式的图形的交点在第三象限?( )
| A. | x-4=0 | B. | x+4=0 | C. | y-4=0 | D. | y+4=0 |
 一只昆虫在如图所示的树枝上寻觅食物,假定昆虫在每个岔路口都会随机选择一条路径,则它获取食物的概率是$\frac{1}{3}$.
一只昆虫在如图所示的树枝上寻觅食物,假定昆虫在每个岔路口都会随机选择一条路径,则它获取食物的概率是$\frac{1}{3}$.
 的值.
的值.
 化简后的结果为( )
化简后的结果为( ) B. -
B. - m C. -
m C. - D. -
D. -