题目内容
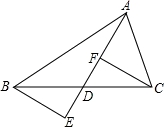
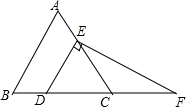
如图,∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=8,则DF等于( )

A.5 B.4 C.3 D.2
B【考点】三角形的外角性质;角平分线的性质;直角三角形斜边上的中线.
【分析】过D作DG⊥AC于G,根据三角形的一个外角等于和它不相邻的两个内角的和求出∠DEG=30°,再根据直角三角形30°角所对的直角边等于斜边的一半求出DG的长度是4,又DE∥AB,所以∠BAD=∠ADE,所以AD是∠BAC的平分线,根据角平分线上的点到角的两边的距离相等,得DF=DG.
【解答】解:如图,∵∠DAE=∠ADE=15°,
∴∠DEG=∠DAE+∠ADE=15°+15°=30°,
DE=AE=8,
过D作DG⊥AC于G,
则DG= DE=
DE= ×8=4,
×8=4,
∵DE∥AB,
∴∠BAD=∠ADE,
∴∠BAD=∠CAD,
∵DF⊥AB,DG⊥AC,
∴DF=DG=4.
故选:B.

【点评】本题主要考查三角形的外角性质,直角三角形30°角所对的直角边等于斜边的一半的性质,平行线的性质和角平分线上的点到角的两边的距离相等的性质,熟练掌握性质是解题的关键.

练习册系列答案
相关题目