Question

6．已知：如图，在⊙O中，弦CD垂直于直径AB，垂足为点E，如果∠BAD=30°，且BE=2，求弦CD的长．

Answer 1

分析 连接OD，设⊙O的半径为r，则OE=r-2，再根据圆周角定理得出∠DOE=60°，由直角三角形的性质可知OD=2OE，由此可得出r的长，在Rt△OED中根据勾股定理求出DE的长，进而可得出结论．

解答 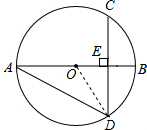解：连接OD，设⊙O的半径为r，则OE=r-2，
∵∠BAD=30°，
∴∠DOE=60°，
∵CD⊥AB，
∴CD=2DE，∠ODE=30°，
∴OD=2OE，即r=2（r-2），解得r=4；
∴OE=4-2=2，
∴DE=$\sqrt{O{D}^{2}-O{E}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$，
∴CD=2DE=4$\sqrt{3}$．

点评 本题考查的是垂径定理，熟知平分弦的直径平分这条弦，并且平分弦所对的两条弧是解答此题的关键．