题目内容
10.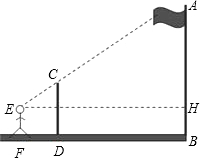 为测量操场上悬挂国旗的旗杆的高度,设计的测量方案如图所示:标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,E,C,A三点共线,求旗杆AB的高度.
为测量操场上悬挂国旗的旗杆的高度,设计的测量方案如图所示:标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,E,C,A三点共线,求旗杆AB的高度.
分析 如图,利用矩形的性质得EF=DG=BH=1.6m,GH=BD=15m,EG=DF=2m,则CG=CD-DG=1.4m,再证明△ECG∽△EAH,利用相似比计算出AH,然后计算AH+BH即可.
解答 解:如图,EF=DG=BH=1.6m,GH=BD=15m,EG=DF=2m,
则CG=CD-DG=3m-1.6m=1.4m,
∵CG∥AH,
∴△ECG∽△EAH,
∴$\frac{CG}{AH}$=$\frac{EG}{EH}$,即$\frac{1.4}{AH}$=$\frac{2}{2+15}$,解得AH=11.9,
∴AB=AH+BH=11.9+1.6=13.5,
答:旗杆AB的高度为13.5m.
点评 本题考查了相似三角形的应用:利用杆或直尺测量物体的高度就是利用杆或直尺的高(长)作为三角形的边,利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度.

练习册系列答案
相关题目
18.张大爷离家出门散步,他先向正东走了80m,接着又向正南走了150m,此时他离家的距离为( )
| A. | 200m | B. | 160 m | C. | 170 m | D. | 180 m |
15.若$\sqrt{x-1}$+(y+2)2=0,则(x+y)2014等于( )
| A. | -2 | B. | 1 | C. | -1 | D. | 2 |
19. 如图,在△ABC中,D在BC上,若AD=BD,AB=AC=CD,则∠ABC的度数是( )
如图,在△ABC中,D在BC上,若AD=BD,AB=AC=CD,则∠ABC的度数是( )
 如图,在△ABC中,D在BC上,若AD=BD,AB=AC=CD,则∠ABC的度数是( )
如图,在△ABC中,D在BC上,若AD=BD,AB=AC=CD,则∠ABC的度数是( )| A. | 30° | B. | 35° | C. | 36° | D. | 60° |
20.若a-(b-c+d)=a-d+( ),则括号中应填入( )
| A. | b-c | B. | b+c | C. | -b+c | D. | -b-c |
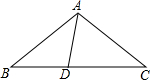 如图,已知,D为△ABC中BC边上一点,∠B=∠C=∠DAB,且∠ADC=∠DAC,求∠BAC的度数.
如图,已知,D为△ABC中BC边上一点,∠B=∠C=∠DAB,且∠ADC=∠DAC,求∠BAC的度数. 画出如图多边形的全部对角线.
画出如图多边形的全部对角线. 如图,已知点M、N和∠AOB,求作一点P,使P到∠AOB两边的距离相等,且到点M、N的距离相等.
如图,已知点M、N和∠AOB,求作一点P,使P到∠AOB两边的距离相等,且到点M、N的距离相等.