题目内容
如图，已知△ABC为等边三角形，点D、E分别在BC、AC边上，且AE=CD，AD与BE相交于点F．
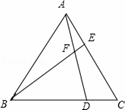（1）求证：△ABE≌△CAD；
（2）求∠BFD的度数．
（1）证明：∵△ABC为等边三角形，
∴∠BAC=∠C=60°，AB=CA，即∠BA
E=∠C=60°，
在△ABE和△CAD中，
，
∴△ABE≌△CAD（SAS）．
（2）解：∵∠BFD=∠ABE+∠BAD，
又∵△ABE≌△CAD，
∴∠ABE=∠CAD．
∴∠BFD=∠CAD+∠BAD=∠BAC=60°．
练习册系列答案
相关题目
_________ 
．
△ABC中，AB=AC，∠A=120°，BC=6cm，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，则MN的长为（ ）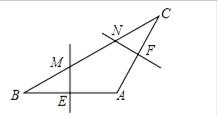
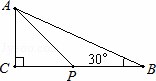
分线，BE平分∠ABD交AD于点E，连接CE．则下列结论：①BE=AE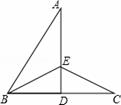
有意义的
的取值范围是（ ）
B．
C．
D．
，母线长
，则该圆锥的侧面积为___________
.