��Ŀ����
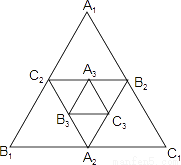
��ͼ��Сǿ�����߳�Ϊ1�ĵ�1���ȱߡ�A1B1C1�����������ΪS1��Ȼ��ֱ�ȡ��A1B1C1���ߵ��е�A2��B2��C1��������2���ȱߡ�A2B2C2�����������ΪS2����ͬ���ķ�����������3���ȱߡ�A3B3C3�����������ΪS3�����˹��ɽ�����ȥ�������ɴ˿ɵã���20���ȱߡ�A20B20C20�����S20=________��
ijУΪ��ѡ��ѧ���μӡ�������д���������Ծ��꼶һ�ࡢ�����10��ѧ�����к�����д���ԣ��Ʒֲ���10���ƣ��÷־�ȡ���������ɼ��ﵽ6�ֻ�6������Ϊ���õ�9��Ϊ���㣬�ɼ����1��ʾ���������˳ɼ�����������2����
��1
һ�� | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 |
���� | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 |
��2
�༶ | ƽ���� | ��λ�� | ���� | ���� | ������ | ������ |
һ�� | 7.6 | 8 | a | 3.82 | 70% | 30% |
���� | b | 7.5 | 10 | 4.94 | 80% | 40% |
��1���ڱ�2�У�a=�� ����b=�� ����
��2������˵����ļ����ʡ������ʾ�����һ�࣬���Զ����һ��ã���Ҳ������Ϊһ��ɼ��ȶ���ã�����������һ��ɼ��õ��������ɣ�
��3��һ�ࡢ��������ֵ���ͬѧ�Ա�ֱ���1��1Ů��2��1Ů���ִ�����������ֵ�ͬѧ�и���1��ͬѧ�μӡ�������д������������״ͼ���б������ǡ�ó鵽1��1Ů��λͬѧ�ĸ��ʣ�
��1��8��7.5����2�����ɼ���������3��P��һ��һŮ��=�� �������������������1���ֱ���ƽ�����ļ��㹫ʽ�������Ķ����ɣ� ��2��һ���ƽ���ɼ��ߣ�����С���ݴ���⣻ ��3���б�����״ͼ�����ø��ʹ�ʽ��⼴�ɣ� ��1��������8������4�Σ���࣬ ������a=8�� b==7.5�� ��2��һ���ƽ���ɼ��ߣ��ҷ���С�����ȶ��� ��һ��ɼ����ڶ��ࣻ ...

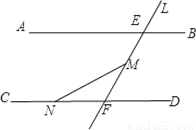

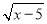 �������x��ȡֵ��Χ��________��
�������x��ȡֵ��Χ��________��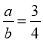 ����
����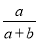 =_____��
=_____��