题目内容
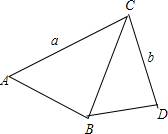 如图所示,已知AB⊥BC,BD⊥CD,AC=a,BC=b.试猜想BD与a,b之间满足怎样的关系时这两个三角形相似?并说明理由.
如图所示,已知AB⊥BC,BD⊥CD,AC=a,BC=b.试猜想BD与a,b之间满足怎样的关系时这两个三角形相似?并说明理由.考点:相似三角形的判定
专题:常规题型
分析:由AB⊥BC,BD⊥CD得到∠ABC=∠BDC=90°,再利用勾股定理计算出AB=
,根据直角三角形相似的判定方法,当
=
,Rt△ABC∽Rt△BDC;当
=
,Rt△ABC∽Rt△CDB,然后分别利用比例性质可表示出BD与a和b的关系.
| a2-b2 |
| AB |
| BD |
| AC |
| BC |
| BC |
| BD |
| AC |
| BC |
解答:解:当BD=
或BD=
时,两个三角形相似.理由如下:
∵AB⊥BC,BD⊥CD,
∴∠ABC=∠BDC=90°,
在Rt△ABC中,∵AC=a,BC=b,
∴AB=
,
当
=
,即
=
,Rt△ABC∽Rt△BDC,所以BD=
;
当
=
,即
=
,Rt△ABC∽Rt△CDB,所以BD=
.
b
| ||
| a |
| b2 |
| a |
∵AB⊥BC,BD⊥CD,
∴∠ABC=∠BDC=90°,
在Rt△ABC中,∵AC=a,BC=b,
∴AB=
| a2-b2 |
当
| AB |
| BD |
| AC |
| BC |
| ||
| BD |
| a |
| b |
b
| ||
| a |
当
| BC |
| BD |
| AC |
| BC |
| b |
| BD |
| a |
| b |
| b2 |
| a |
点评:本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;两组对应边的比相等的两个直角三角形相似.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 有理数a,b在数轴上的位置如图,则下列各式中正确的是( )
有理数a,b在数轴上的位置如图,则下列各式中正确的是( )| A、a+b<0 | B、a-b<0 |
| C、|b|>a | D、ab<0 |
 如图,请在下列网格图中画出所给图形绕点O顺时针依次旋转90°后所成的图形.
如图,请在下列网格图中画出所给图形绕点O顺时针依次旋转90°后所成的图形. 如图,身高1.5m的小明用一个两锐角分别是30°和60°的三角尺测量一棵树的高度,已知他与树之间的距离为5米,求这棵树的高度.(精确到0.1米)
如图,身高1.5m的小明用一个两锐角分别是30°和60°的三角尺测量一棵树的高度,已知他与树之间的距离为5米,求这棵树的高度.(精确到0.1米) 如图,延长正方形ABCD的一边CB至E,ED与AB相交于点F,过F作FG∥BE交AE于点G,求证:GF=FB.
如图,延长正方形ABCD的一边CB至E,ED与AB相交于点F,过F作FG∥BE交AE于点G,求证:GF=FB.