题目内容
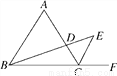
如图,△ABC是等边三角形,CE是∠ACB的外角平分线,点D在AC上,连接BD并延长交CE于点E.
(1)求证:△ABD∽△CED;
(2)若AB=6,AD=2CD,求BE的长.
练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
王勇和李明两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了30次实验,实验的结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 2 | 5 | 6 | 4 | 10 | 3 |
(1)分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率;
(2)王勇说:“根据以上实验可以得出结论:由于5点朝上的频率最大,所以一次实验中出现5点朝上的概率最大”;李明说:“如果投掷300次,那么出现6点朝上的次数正好是30次”.试分别说明王勇和李明的说法正确吗?并简述理由;
(3)现王勇和李明各投掷一枚骰子,请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
(1); (2)王勇的说法是错误的,李明的说法也是错误的(3) 【解析】试题分析:(1)、根据概率的计算法则分别求出“3点朝上”和“5点朝上”的概率;(2)、根据随机事件的性质来分别进行说明;(3)、首先将所得的所有结果用列表法来表示出来,然后找出符合条件的情况,最后根据概率的计算法则求出答案. 试题解析:(1)“3点朝上”的频率为:, “5点朝上”的频率为:; (2)王勇...

 B、
B、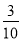 C、
C、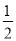 D、
D、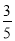
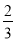 .则点A的对应点A′的坐标为____________.
.则点A的对应点A′的坐标为____________.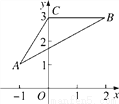
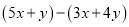 ,其中
,其中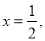
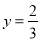 .
.