题目内容
1.已知,Rt△ABC中,∠C=90°,AC=6,AB=10,则三角形内切圆的半径为2.分析 先根据勾股定理计算出BC,然后利用直角边为a、b,斜边为c的三角形的内切圆半径为$\frac{a+b+c}{2}$进行计算.
解答 解:∵∠C=90°,AC=6,AB=10,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴△ABC的内切圆半径r=$\frac{6+8-10}{2}$=2.
故答案是:2.
点评 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.记住直角边为a、b,斜边为c的三角形的内切圆半径为$\frac{a+b-c}{2}$.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
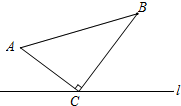 如图,△ABC中,∠ACB=90°,AC=8cm,BC=15cm,点P从A点出发沿A→C→B路径向终点运动,终点为B点,点Q从B点出发沿B→C→A路径向终点运动,终点为A点,点P和Q分别以1cm/s和3cm/s的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F,问:点P运动多少时间内,△PEC与△QFC相似且相似比为$\frac{4}{3}$?请说明理由.
如图,△ABC中,∠ACB=90°,AC=8cm,BC=15cm,点P从A点出发沿A→C→B路径向终点运动,终点为B点,点Q从B点出发沿B→C→A路径向终点运动,终点为A点,点P和Q分别以1cm/s和3cm/s的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F,问:点P运动多少时间内,△PEC与△QFC相似且相似比为$\frac{4}{3}$?请说明理由.