题目内容

19．已知关于x的分式方程$\frac{m-2}{x-2}+\frac{3}{2-x}=1$的解为非负数，则m的取值范围为m≥3且m≠5．

分析 根据解分式方程，可得分式方程的解，根据分式方程的解为负数，可得不等式，解不等式，可得答案．

解答 解：去分母，得：m-2-3=x-2，
移项、合并，得：x=m-3，
∵分式方程的解为非负数，
∴m-3≥0且m-3≠2，
解得：m≥3且m≠5，
故答案为：m≥3且m≠5．

点评 本题考查了分式方程的解，先求出分式方程的解，再求出不等式的解．

练习册系列答案
相关题目
3．2015年4月9日交通运输部报道，韵达速递（简称“韵达”）与上海良友便利连锁有限公司（简称“良友”）展开合作，为良友提供“社区商品配送”服务，某天韵达快递员骑摩托车从良友便利店出发，先向北行驶3km到达A村，继续向北行驶2km到达B村，然后向南行驶7km到达C村，最后回到便利店．
（1）画一个数轴，该数轴以便利店为原点，向北行驶的方向为正方向，用1个单位长度表示1km，请你在数轴上表示出A，B，C三个村庄的位置；
（2）A村离C村有多远？
（3）求该天韵达快递员一共行驶的路程．
4．若a，b，c为整数，且|a-b|+|c-a|=1，试计算|c-a|+|a-b|+|b-c|的值．
7．如图，有一块三角形材料（△ABC），请你画出一个半圆，使得圆心在线段AC上，且与AB、BC相切．
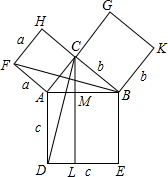14．△ABC是以∠ACB为直角的直角三角形，以AB、BC、AC为边作正方形ABED、BCGK、ACHF，过点C作CL⊥DE交AB于点M，交DE于点L，连接CD、BF．求证：a2+b2=c2．
4．点P与点Q位于线段MN的两侧，
（1）如图甲，若△PMN和△QMN中，PI平分外角∠SPN，并与线段MN的延长线交于点I，连接QI，若△PMN≌△QMN，求证：QI平分外角∠TQN；
（2）如图乙，若△PMN和△QMN中，PM+PN=QM+QN，且外角∠SPN和∠TQN的角平分线PI、QI相交于点I，连接MI，求证：MI平分∠PMQ．
11．如果把分式$\frac{a+2b}{ab}$中的a和b都扩大2倍，即分式的值（　　）
A．扩大4倍B．扩大2倍C．不变D．缩小2倍
8．平面直角坐标系中，若P1（x1，y1），P2（x2，y2），则线段P1P2的中点坐标可表示为（$\frac{{x}_{1}+{x}_{2}}{2}$，$\frac{{y}_{1}+{y}_{2}}{2}$），例如P1（-1，3），P2（5，1），则P1P2的中点坐标为（2，2），如图1，直线y=2x+2与直线y=-2x+14交于点M，分别交x轴于点A和点B，动点C（0，n）在y轴正半轴上运动，动点P（m，0）从原点O出发沿x轴的正方向运动到点B，过点C作CD∥x轴交直线MB于点D，以P，C，D为顶点作?PDQC，PQ与CD交于点E
（1）当n=4时，点D的坐标为（5，4）．
（2）如图2，当n=2时，解决下列问题：
①点E坐标是（3，2）；
②当?PDQC是菱形时，m=3；当点Q落在y轴上时，m=6；
③当点Q落在MB上时记为Q1，点Q落在MA上时记为Q2，求点Q从Q1运动到Q2的过程中，线段PQ扫过的面积．
（3）在点P从点O到B的运动过程中，若点Q始终落在△MAB外，请直接写出n取值范围．
9．已知抛物线y=$\frac{1}{2}$x2+x+m与x轴交于A，B两点，与y轴交于点C．
（1）求m的取值范围；
（2）当AB=4时，在该抛物线上是否存在点P，使得△ABP的面积是△ABC的面积的2倍？若存在，求出点P的坐标；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网