题目内容
19. 如图,在直角坐标系中,一条抛物线与x轴交于A、B两点,与y轴交于C点,其中B(3,0),C(0,4),点A在x轴的负半轴上,OC=4OA;
如图,在直角坐标系中,一条抛物线与x轴交于A、B两点,与y轴交于C点,其中B(3,0),C(0,4),点A在x轴的负半轴上,OC=4OA;(1)求这条抛物线的解析式,并求出它的顶点坐标;
(2)联结AC、BC,点P是x轴正半轴上一个动点,过点P作PM∥BC交射线AC于点M,联结CP,若△CPM的面积为2,则请求出点P的坐标.
分析 (1)根据OA与OC的关系,可得A点坐标,根据待定系数法,可得函数解析式;
(2)根据锐角三角函数,可得PH的长,根据相似三角形的性质,可得MC的长,根据三角形的面积,可得关于x的方程,根据解方程,可得答案.
解答 解:(1)∵C(0,4),O(0,0),
∴OC=4.
∵OC=4OA,
∴OA=1.
∵点A在x轴的负半轴上,
∴A(-1,0).
设这条抛物线的解析式为y=ax2+bx+c,
∵抛物线过点 A(-1,0),B(3,0),C(0,4)
∴$\left\{\begin{array}{l}a-b+c=0\\ 9a+3b+c=0\\ c=4\end{array}\right.$,
解得$\left\{\begin{array}{l}a=-\frac{4}{3}\\ b=\frac{8}{3}\\ c=4\end{array}\right.$,
∴这条抛物线的解析式为y=-$\frac{4}{3}$x2+$\frac{8}{3}$x+4,
它的顶点坐标为(1,$\frac{16}{3}$);
(2)过点P作PH⊥AC,垂足为H.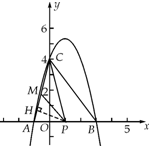
∵P点在x轴的正半轴上,
∴设P(x,0).
∵A(-1,0),
∴PA=x+1.
∵在Rt△AOC中,OA2+OC2=AC2
又∵OA=1,OC=4,
∴AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,
∵∠AOC=90°,
∴sin∠CAO=$\frac{OC}{OA}$=$\frac{4}{\sqrt{17}}$=$\frac{4\sqrt{17}}{17}$
∵∠PHA=90°,
∴sin∠CAO=$\frac{PH}{AP}$=$\frac{PH}{x+1}$=$\frac{4\sqrt{17}}{17}$
∴PH=$\frac{4\sqrt{17}(x+1)}{17}$.
∵PM∥BC,
∴$\frac{BP}{AB}$=$\frac{CM}{AC}$
∵B(3,0),P(x,0)
①点P在点B的左侧时,BP=3-x
∴$\frac{3-x}{4}$=$\frac{CM}{\sqrt{17}}$,
∴CM=$\frac{\sqrt{17}(3-x)}{4}$.
∵S△PCM=2,
∴$\frac{1}{2}$CM•PH=2,
∴$\frac{1}{2}$•$\frac{\sqrt{17}(3-x)}{4}$•$\frac{4\sqrt{17}(x+1)}{17}$=2.
解得x=1.
∴P(1,0);
②点P在点B的右侧时,BP=x-3
∴$\frac{x-3}{4}$=$\frac{CM}{\sqrt{17}}$,
∴CM=$\frac{\sqrt{17}(3-x)}{4}$,
∵S△PCM=2,
∴$\frac{1}{2}$CM•PH=2,
∴$\frac{1}{2}$•$\frac{\sqrt{17}(3-x)}{4}$•$\frac{4\sqrt{17}(x+1)}{17}$=2.
解得x1=1+2$\sqrt{2}$,x2=1-2$\sqrt{2}$(不合题意,舍去)
∴P($1+2\sqrt{2}$,0).
综上所述,P的坐标为(1,0)或($1+2\sqrt{2}$,0).
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式;利用锐角三角函数得出PH的长是解题关键,又利用相似三角形的性质得出CM的长,利用三角形的面积得出关于x的方程.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 B.
B. 
 D.
D. 

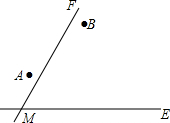 两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部
两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部 B.
B.  C.
C.  D.
D. 