题目内容
14.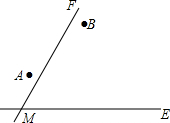 两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部
两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部(1)那么点C应选在何处?请在图中,用尺规作图找出符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)
(2)设AB的垂直平分线交ME于点N,且MN=2($\sqrt{3}$+1)km,测得∠CMN=30°,∠CNM=45°,求点C到公路ME的距离.
分析 (1)运用尺规作图即可得出结果;
(2)作CD⊥MN于点D.由三角函数得出MD=$\sqrt{3}$CD,DN=$\frac{CD}{tan45°}$=CD,由已知条件得出$\sqrt{3}$CD+CD=2($\sqrt{3}$+1),解得CD=2km即可.
解答 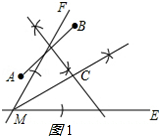 解:(1)答图如图1所示:
解:(1)答图如图1所示:
点C即为所求;
(2)作CD⊥MN于点D.如图2所示:
∵在Rt△CMD中,∠CMN=30°,
∴$\frac{CD}{MD}$=tan∠CMN,
∴MD=$\frac{CD}{tan30°}$=$\frac{CD}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$CD,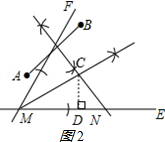 ∵在Rt△CND中,∠CNM=45°,$\frac{CD}{DN}$=tan∠CNM,
∵在Rt△CND中,∠CNM=45°,$\frac{CD}{DN}$=tan∠CNM,
∴DN=$\frac{CD}{tan45°}$=CD,∵MN=2($\sqrt{3}$+1)km,
∴MN=MD+DN=$\sqrt{3}$CD+CD=2($\sqrt{3}$+1)km.
解得:CD=2km.
答:点C到公路ME的距离为2km.
点评 本题考查了解直角三角形的应用、作图-设计;熟练掌握基本作图和解直角三角形是解决问题的关键.

练习册系列答案
相关题目
8.永川重百商场为庆祝“元旦”,特搞促销活动,有两件进价不同的衣服均卖了80元,其中一件盈利60%,另一件亏本20%,这次买卖交易中商家( )
| A. | 不赔不赚 | B. | 赚了8元 | C. | 赚了10元 | D. | 赚了32元 |
9.在数轴上与表示-3的点距离等于5的点所表示的数是( )
| A. | 1 | B. | 2和8 | C. | -8 | D. | -8和2 |
6.计算$\sqrt{2013×2014×2015×2016+1}$-20142=( )
| A. | 2013 | B. | 2014 | C. | 2015 | D. | 2016 |
 如图,在直角坐标系中,一条抛物线与x轴交于A、B两点,与y轴交于C点,其中B(3,0),C(0,4),点A在x轴的负半轴上,OC=4OA;
如图,在直角坐标系中,一条抛物线与x轴交于A、B两点,与y轴交于C点,其中B(3,0),C(0,4),点A在x轴的负半轴上,OC=4OA;