��Ŀ����
����С������12�֣����ڶ��κ���y=x²��3x+2��һ�κ���y=��2x+4����y=t��x²��3x+2��+��1��t������2x+4����Ϊ�����������ġ��������κ�����������t�Dz�Ϊ���ʵ������ͼ�����������L.���е�A��2��0����������L�ϵĵ�B����1��n�����������������
�����ԡ�
��1����t=2ʱ��������y=t��x²��3x+2��+��1��t������2x+4���Ķ�������Ϊ ��
��2���жϵ�A�Ƿ���������L�ϣ�
��3����n��ֵ��
�����֡�
ͨ����2���ͣ�3���������֪������tȡ�κβ�Ϊ���ʵ����������L�ܹ����㣬����Ϊ .
��Ӧ�á�
���κ���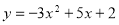 �Ƕ��κ���y=x²��3x+2��һ�κ���y=��2x+4��һ�����������κ�����������ǣ����t��ֵ��������ǣ�˵������
�Ƕ��κ���y=x²��3x+2��һ�κ���y=��2x+4��һ�����������κ�����������ǣ����t��ֵ��������ǣ�˵������
��1����1����2������2����A��2��0����������E�ϣ���3��n=6����4��������E�ع����㣨2��0��������1��6������5����������������t��ֵΪ���� ��
�� ����
���� ��
��
��������
��������������ԡ���1����t��ֵ���롰�������κ������У�ͨ���䷽�ɵõ���������ꣻ
��2������A���������������E��ֱ�ӽ�����֤���ɣ�
��3����֪��B��������E�ϣ����õ��������������E�Ľ���ʽ��ֱ����⣬���ɵõ�n��ֵ��
�����֡���������Eչ����Ȼ��tֵ��ʽ�����ϵ�һ�����ʽ��Ϊ0����ʱ����tȡ��ֵ������Ժ���ֵ����Ӱ�죩��������������������꣮
��Ӧ��1���������֡��еõ��������������������κ���y=��3x2+5x+2�н�����֤���ɣ�
��Ӧ��2������Ĺؼ������C��D�����ꣻ���Ȼ�����Ӧ��ͼ�Σ���C��D��������Ĵ��ߣ�ͨ���������������λ�ȫ������������⣮�����C��D���������֪������E�ع�A��B�����ֻ�轫C��D���������������E�Ľ���ʽ�У������������������tֵ��
��������������ԡ���1����t=2����������E�У��ã�y=t��x2��3x+2��+��1��t������2x+4��=2x2��4x=2��x��1��2��2��
���ʱ�����ߵĶ�������Ϊ����1����2����
��2����x=2����y=t��x2��3x+2��+��1��t������2x+4������ y=0��
���A��2��0����������E�ϣ�
��3����x=��1����������E�Ľ���ʽ�У��ã�
n=t��x2��3x+2��+��1��t������2x+4��=6��
�����֡���������E�Ľ���ʽչ�����ã�
y=t��x2��3x+2��+��1��t������2x+4��=t��x��2����x+1����2x+4
��������E�ع����㣨2��0��������1��6����
��Ӧ��1����x=2����y=��3x2+5x+2��y=0������A���������ϣ�
��x=��1����y=��3x2+5x+2������ã�y=��6��6��
���ɵ�������y=��3x2+5x+2��������B��
���κ���y=��3x2+5x+2���Ƕ��κ���y=x2��3x+2��һ�κ���y=��2x+4��һ�����������κ�������
��Ӧ��2����ͼ��������ABC1D1��ABC2D2������B��BK��y���ڵ�K����B��BM��x���ڵ�M��
��AM=3��BM=6��BK=1����KBC1�ס�MBA��
�� ����
���� ����� C1K=
����� C1K= �����Ե�C1��0��
�����Ե�C1��0�� ����
����
��֪��KBC1�ա�GAD1����AG=1��GD1= ��
��
���D1��3�� ����
����
��֪��OAD2�ס�GAD1�� ��AG=1��OA=2��GD1=
��AG=1��OA=2��GD1= ����� OD2=1�����D2��0����1����
����� OD2=1�����D2��0����1����
��֪��TBC2�ա�OD2A����TC2=AO=2��BT=OD2=1�����Ե�C2����3��5����
��������E�ܹ�����A��2��0����B����1��6����
��������������������A��B��C��A��B��D��
��������E����A��B��C1ʱ����C1��0�� ������y=t��x2��3x+2��+��1��t������2x+4�������t1=��
������y=t��x2��3x+2��+��1��t������2x+4�������t1=�� ��
��
��������E����A��B��D1��A��B��C2��A��B��D2ʱ���ɷֱ����t2= ��t3=��
��t3=�� ��t4=
��t4= ��
��
����������������t��ֵΪ���� ��
�� ����
���� ��
�� ��
��

���㣺���κ����ۺ���

 ������ȫ��������ϵ�д�
������ȫ��������ϵ�д�
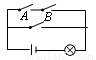
 ������kΪ������,�ֱ�ȡx1=��0.99��x2=0.98��x3=0.99ʱ��Ӧ�ĺ���ֵ�ֱ�Ϊy1, y2, y3���뽫y1, y2, y3�á�<����������__ __.
������kΪ������,�ֱ�ȡx1=��0.99��x2=0.98��x3=0.99ʱ��Ӧ�ĺ���ֵ�ֱ�Ϊy1, y2, y3���뽫y1, y2, y3�á�<����������__ __.
 ��ͼ����x���һ����������Ϊ(3,0)������һ����ĺ�����Ϊ�� ��
��ͼ����x���һ����������Ϊ(3,0)������һ����ĺ�����Ϊ�� ��
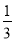 ��B��
��B��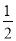 ��C��
��C��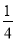 ��D��
��D��