题目内容
将抛物线y1=x2向右平移2个单位,得到抛物线y2的图象.P是抛物线y2对称轴上的一个动点,直线x=t平行于y轴,分别与直线y =x、抛物线y2交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则t= .


【解析】
试题分析:∵抛物线y1=x2向右平移2个单位,
∴抛物线y2的函数解析式为y=(x﹣2)2=x2﹣4x+4,
∴抛物线y2的对称轴为直线x=2,
∵直线x=t与直线y=x、抛物线y2交于点A、B,
∴点A的坐标为(t,t),点B的坐标为(t,t2﹣4t+4),
∴AB=|t2﹣4t+4﹣t|=|t2﹣5t+4|,
AP=|t﹣2|,
∵△APB是以点A或B为直角顶点的三角形,
∴|t2﹣5t+4|=|t﹣2|,
∴t2﹣5t+4=t﹣2①或t2﹣5t+4=﹣(t﹣2)②,
整理①得,t2﹣6t+6=0,
解得t1=3+ ,t2=3﹣
,t2=3﹣ ,
,
整理②得,t2﹣4t+2=0,
解得t1=2+ ,t2=2﹣
,t2=2﹣ ,
,
综上所述,满足条件的t值为:
考点:二次函数图象与几何变换

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案
相关题目
根据下列表格中二次函数y=Ax2+Bx+C的自变量与函数值的对应值,判断方程Ax2+B x+C=0(A≠0)的一个解的范围是( )
| 6.17 | 6.18 | 6.19 | 6.20 |
y=Ax2+B x+C |
|
|
|
|
A.6<x<6.17 B.6.17<x<6.18
C.6.18<x<6.19 D.6.19<x<6.20
 与直线
与直线 交于A、B两点(点A在点B的左侧),动点P从A点出发,先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到点B.若使点P运动的总路径最短,则点P运动的总路径的长为( )
交于A、B两点(点A在点B的左侧),动点P从A点出发,先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到点B.若使点P运动的总路径最短,则点P运动的总路径的长为( ) B.
B. C.
C. D.
D.




 的对称轴为
的对称轴为 ,交
,交 轴的一个交点为(
轴的一个交点为( ,0),且
,0),且 , 则下列结论:①
, 则下列结论:① ,
, ;②
;② ;③
;③ ; ④
; ④ ,⑤
,⑤ . 其中正确的命题有( )个.
. 其中正确的命题有( )个. 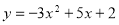 是二次函数y=x²-3x+2和一次函数y=-2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由
是二次函数y=x²-3x+2和一次函数y=-2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由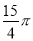 cm B.
cm B. 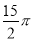 cm C.
cm C. 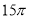 cm D.
cm D. 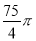 cm
cm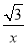 上的点B重合,若点B的纵坐标是1,则点A的坐标是
上的点B重合,若点B的纵坐标是1,则点A的坐标是 
