题目内容
按要求解下列方程:
(1)x2+x-1=0(用配方法解);
(2)4x2-8x=1.
(1)x2+x-1=0(用配方法解);
(2)4x2-8x=1.
考点:解一元二次方程-配方法
专题:计算题
分析:(1)方程常数项移到右边,两边加上一次项系数一半的平方,利用完全平方公式变形,开方即可求出解;
(2)方程二次项系数化为1,常数项移到右边,两边加上一次项系数一半的平方,利用完全平方公式变形,开方即可求出解.
(2)方程二次项系数化为1,常数项移到右边,两边加上一次项系数一半的平方,利用完全平方公式变形,开方即可求出解.
解答:解:(1)方程变形得:x2+x=1,
配方得:x2+x+
=
,即(x+
)2=
,
开方得:x+
=±
,
解得:x1=
,x2=
;
(2)方程变形得:x2-2x=
,
配方得:x2-2x+1=
,即(x-1)2=
,
开方得:x-1=±
,
解得:x1=1+
,x2=1-
.
配方得:x2+x+
| 1 |
| 4 |
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
开方得:x+
| 1 |
| 2 |
| ||
| 2 |
解得:x1=
-1+
| ||
| 2 |
-1-
| ||
| 2 |
(2)方程变形得:x2-2x=
| 1 |
| 4 |
配方得:x2-2x+1=
| 5 |
| 4 |
| 5 |
| 4 |
开方得:x-1=±
| ||
| 2 |
解得:x1=1+
| ||
| 2 |
| ||
| 2 |
点评:此题考查了解一元二次方程-配方法,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在正方形ABCD中,边AB上有一点M,其中AM=3BM,N是AD上一点,且AN=ND,判断△MNC是否是直角三角形,并说明理由.
如图,在正方形ABCD中,边AB上有一点M,其中AM=3BM,N是AD上一点,且AN=ND,判断△MNC是否是直角三角形,并说明理由. 如图,在矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,求CF的长.
如图,在矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,求CF的长.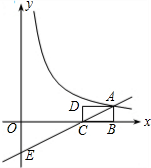 如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx-2的图象经过点A、C,并与y轴交于点E.反比例函数
如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx-2的图象经过点A、C,并与y轴交于点E.反比例函数 已知如图,三条直线AB、CD、EF交于一点,若∠1=30°,∠2=70°,求∠3的度数.
已知如图,三条直线AB、CD、EF交于一点,若∠1=30°,∠2=70°,求∠3的度数.