题目内容
19.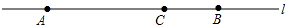 如图,已知点A、点B是直线上的两点,AB=12厘米,点C在线段AB上,且AC=8厘米.点P、点Q是直线上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.点P、Q分别从点C、点B同时出发,在直线上运动,则经过2、10、$\frac{2}{3}$或$\frac{10}{3}$秒时线段PQ的长为6厘米.
如图,已知点A、点B是直线上的两点,AB=12厘米,点C在线段AB上,且AC=8厘米.点P、点Q是直线上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.点P、Q分别从点C、点B同时出发,在直线上运动,则经过2、10、$\frac{2}{3}$或$\frac{10}{3}$秒时线段PQ的长为6厘米.
分析 首先根据AB=12厘米,AC=8厘米,求出CB的长度是多少;然后分四种情况:(1)点P、Q都向右运动;(2)点P、Q都向左运动;(3)点P向左运动,点Q向右运动;(4)点P向右运动,点Q向左运动;求出经过多少秒时线段PQ的长为6厘米即可.
解答 解:∵AB=12厘米,AC=8厘米,
∴CB=12-8=4(厘米);
(1)点P、Q都向右运动时,
(6-4)÷(2-1)
=2÷1
=2(秒)
(2)点P、Q都向左运动时,
(6+4)÷(2-1)
=10÷1
=10(秒)
(3)点P向左运动,点Q向右运动时,
(6-4)÷(2+1)
=2÷3
=$\frac{2}{3}$(秒)
(4)点P向右运动,点Q向左运动时,
(6+4)÷(2+1)
=10÷3
=$\frac{10}{3}$(秒)
∴经过2、10、$\frac{2}{3}$或$\frac{10}{3}$秒时线段PQ的长为6厘米.
故答案为:2、10、$\frac{2}{3}$或$\frac{10}{3}$.
点评 此题主要考查了两点间的距离的求法,以及分类讨论思想的应用,要熟练掌握.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
10.某种商品的标价为132元.若以标价的9折出售,仍可获利10%,则该商品的进价( )
| A. | 105元 | B. | 100元 | C. | 108元 | D. | 118元 |
7.8-(-7)的值是( )
| A. | 15 | B. | -1 | C. | -15 | D. | 1 |
14.下列选项中是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4. 如图,△ABC的两条中线AD、CE交于点G,且AD⊥CE,联结BG并延长与AC交于点F,如果AD=9,CE=12,那么下列结论不正确的是( )
如图,△ABC的两条中线AD、CE交于点G,且AD⊥CE,联结BG并延长与AC交于点F,如果AD=9,CE=12,那么下列结论不正确的是( )
 如图,△ABC的两条中线AD、CE交于点G,且AD⊥CE,联结BG并延长与AC交于点F,如果AD=9,CE=12,那么下列结论不正确的是( )
如图,△ABC的两条中线AD、CE交于点G,且AD⊥CE,联结BG并延长与AC交于点F,如果AD=9,CE=12,那么下列结论不正确的是( )| A. | AC=10 | B. | AB=15 | C. | BG=10 | D. | BF=15 |
 如图,AB=5cm,BC=3cm,如果O是线段AC的中点,求线段OB=1cm.
如图,AB=5cm,BC=3cm,如果O是线段AC的中点,求线段OB=1cm.
