题目内容
圆的两条半径把圆分成两个扇形,它们的面积比为
,且较大扇形的面积等于π,那么圆的半径等于 .
| 7 |
| 2 |
考点:扇形面积的计算
专题:
分析:根据两个扇形的面积之比为
,分别设两个扇形的面积为7k、2k;求出k的值;利用圆的面积公式即可解决问题.
| 7 |
| 2 |
解答:解:∵圆的两条半径把圆分成两个扇形,它们的面积比为
,
∴若设较大扇形的面积为7k,则较小扇形的面积为2k;
∵较大扇形的面积为π,∴7k=π,k=
π;
设圆的半径为r,则πr2=
π×9,
解得r=
,
故答案为
.
| 7 |
| 2 |
∴若设较大扇形的面积为7k,则较小扇形的面积为2k;
∵较大扇形的面积为π,∴7k=π,k=
| 1 |
| 7 |
设圆的半径为r,则πr2=
| 1 |
| 7 |
解得r=
3
| ||
| 7 |
故答案为
3
| ||
| 7 |
点评:该题考查了扇形面积的计算问题;解题的关键是设出参数,灵活运用扇形或圆的面积公式来解题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
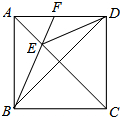 如图,在正方形ABCD中,E为对角线AC上一点,连结EB,ED,BD,延长BE交AD于点F,DF2=EF•BF.
如图,在正方形ABCD中,E为对角线AC上一点,连结EB,ED,BD,延长BE交AD于点F,DF2=EF•BF. 如图,在△ABC中,AC、BC边上的高BE、AD交于H,若HA=3,AE=2,求tan∠C的值.
如图,在△ABC中,AC、BC边上的高BE、AD交于H,若HA=3,AE=2,求tan∠C的值.