题目内容
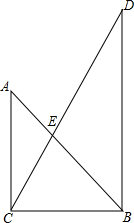 两块直角三角形如图所示放置,其中∠ACB=∠CBD=90°,∠A=45°,∠D=30°,若BC=1,求S△ACE:S△BDE.
两块直角三角形如图所示放置,其中∠ACB=∠CBD=90°,∠A=45°,∠D=30°,若BC=1,求S△ACE:S△BDE.考点:相似三角形的判定与性质
专题:
分析:根据条件可证明△ACE∽△BDE,由BC=1可求得AC和BD,再利用相似三角形的面积比等于相似比的平方可求得答案.
解答:解:∵∠ACB=∠CBD=90°,
∴AC∥BD,
∴∠A=∠DBE,∠ACE=∠D,
∴△ACE∽△BDE,
∵∠A=45°,∠D=30°,BC=1,
∴AC=BC=1,BD=
BC=
,
∴
=(
)2=(
)2=
,
∴S△ACE:S△BDE=1:3.
∴AC∥BD,
∴∠A=∠DBE,∠ACE=∠D,
∴△ACE∽△BDE,
∵∠A=45°,∠D=30°,BC=1,
∴AC=BC=1,BD=
| 3 |
| 3 |
∴
| S△ACE |
| S△BDE |
| AC |
| BD |
| 1 | ||
|
| 1 |
| 3 |
∴S△ACE:S△BDE=1:3.
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若
-
=2a-6,则a的取值范围为( )
| (1-a)2 |
| a2-10a+25 |
| A、a为任意实数 | B、1≤a≤5 |
| C、a≥1 | D、a≤5 |
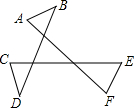 我们知道:“在三角形的每个顶点处各取一个外角,它们的和就是这个三角形的外角和”.
我们知道:“在三角形的每个顶点处各取一个外角,它们的和就是这个三角形的外角和”.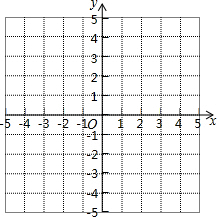 已知点A(0,0),B(2,0),点C在y轴上,且S△ABC=3.
已知点A(0,0),B(2,0),点C在y轴上,且S△ABC=3.