题目内容
 我们知道:“在三角形的每个顶点处各取一个外角,它们的和就是这个三角形的外角和”.
我们知道:“在三角形的每个顶点处各取一个外角,它们的和就是这个三角形的外角和”.(1)猜想三角形的外角和是多少度?证明你的结论;
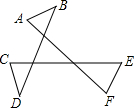
(2)如果将三角形三条边都向两边延长,并且在每条线上任取两点连接起来,那么在原三角形外又得到三个新三角形,如图所示,猜想∠A、∠B、∠C、∠D、∠E、∠F的和是多少?并用(1)的结论证明你的猜想.
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)先利用三角形外角性质得到∠1=∠ABC+∠ACB,∠2=∠ABC+∠BAC,∠3=∠ACB+∠BAC,再把它们相加,然后根据三角形内角和可得到∠1+∠2+∠3=360°;
(2)先根据三角形外角的性质得出∠AGM=∠A+∠B,∠MNF=∠E+∠F,∠DMN=∠C+∠D,再由(1)中的结论即可得出结果.
(2)先根据三角形外角的性质得出∠AGM=∠A+∠B,∠MNF=∠E+∠F,∠DMN=∠C+∠D,再由(1)中的结论即可得出结果.
解答: (1)三角形的外角和等于360°.
(1)三角形的外角和等于360°.
证明:如图所示,
∵∠1是△ABC的外角,
∴∠1=∠ABC+∠ACB,
同理得∠2=∠ABC+∠BAC,∠3=∠ACB+∠BAC,
∴∠1+∠2+∠3=(∠ABC+∠ACB)+(∠ABC+∠BAC)+(∠ACB+∠BAC),
=2(∠ABC+∠ACB+∠BAC)
∵∠ABC+∠ACB+∠BAC=180°,
∴∠1+∠2+∠3=360°.

(2)猜想:∠A+∠B+∠C+∠D+∠E+∠F=360°.
证明:∵∠AGM是△ABG的外角,
∴∠AGM=∠A+∠B.
∵∠MNF是△EFN的外角,
∴∠MNF=∠E+∠F.
∵∠DMN是△CDM的外角,
∴∠DMN=∠C+∠D.
∵∠AGM,∠MNF,∠DMN是△GMN的外角,
∴∠AGM+∠MNF+∠DMN=360°,即∠A+∠B+∠C+∠D+∠E+∠F=360°.
 (1)三角形的外角和等于360°.
(1)三角形的外角和等于360°.证明:如图所示,
∵∠1是△ABC的外角,
∴∠1=∠ABC+∠ACB,
同理得∠2=∠ABC+∠BAC,∠3=∠ACB+∠BAC,
∴∠1+∠2+∠3=(∠ABC+∠ACB)+(∠ABC+∠BAC)+(∠ACB+∠BAC),
=2(∠ABC+∠ACB+∠BAC)
∵∠ABC+∠ACB+∠BAC=180°,
∴∠1+∠2+∠3=360°.

(2)猜想:∠A+∠B+∠C+∠D+∠E+∠F=360°.
证明:∵∠AGM是△ABG的外角,
∴∠AGM=∠A+∠B.
∵∠MNF是△EFN的外角,
∴∠MNF=∠E+∠F.
∵∠DMN是△CDM的外角,
∴∠DMN=∠C+∠D.
∵∠AGM,∠MNF,∠DMN是△GMN的外角,
∴∠AGM+∠MNF+∠DMN=360°,即∠A+∠B+∠C+∠D+∠E+∠F=360°.
点评:本题考查的是三角形内角和定理及三角形外角的性质,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
在Rt△ABC中,已知sinA=
,则∠A的对边为( )
| 3 |
| 5 |
| A、3 | B、4 | C、5 | D、无法确定 |
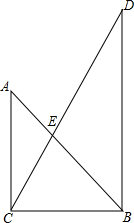 两块直角三角形如图所示放置,其中∠ACB=∠CBD=90°,∠A=45°,∠D=30°,若BC=1,求S△ACE:S△BDE.
两块直角三角形如图所示放置,其中∠ACB=∠CBD=90°,∠A=45°,∠D=30°,若BC=1,求S△ACE:S△BDE.