题目内容
△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,则∠FDE与 ∠A的关系是
∠A的关系是
- A.∠FDE+
 ∠A=90°
∠A=90° - B.∠FDE=
 ∠A
∠A - C.∠FDE+
 ∠A=180°
∠A=180° - D.无法确定
A
分析:连接IE,IF,则有∠IEA=∠IFA=90°,∠EIF=180°-∠A,由圆周角定理知,∠FDE= ∠EIF=90°-
∠EIF=90°- ∠A,所以可求得∠FDE+
∠A,所以可求得∠FDE+ ∠A=90°.
∠A=90°.
解答: 解:连接IE,IF,则有∠IEA=∠IFA=90°,
解:连接IE,IF,则有∠IEA=∠IFA=90°,
∴∠EIF=180°-∠A,
∴∠FDE= ∠EIF=90°-
∠EIF=90°- ∠A,
∠A,
∴∠FDE+ ∠A=90°.
∠A=90°.
故选A.
点评:本题利用了切线的概念,圆周角定理求解.
分析:连接IE,IF,则有∠IEA=∠IFA=90°,∠EIF=180°-∠A,由圆周角定理知,∠FDE=
 ∠EIF=90°-
∠EIF=90°- ∠A,所以可求得∠FDE+
∠A,所以可求得∠FDE+ ∠A=90°.
∠A=90°.解答:
 解:连接IE,IF,则有∠IEA=∠IFA=90°,
解:连接IE,IF,则有∠IEA=∠IFA=90°,∴∠EIF=180°-∠A,
∴∠FDE=
 ∠EIF=90°-
∠EIF=90°- ∠A,
∠A,∴∠FDE+
 ∠A=90°.
∠A=90°.故选A.
点评:本题利用了切线的概念,圆周角定理求解.

练习册系列答案
相关题目
△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,则∠FDE与
∠A的关系是( )
| 1 |
| 2 |
A、∠FDE+
| ||
B、∠FDE=
| ||
C、∠FDE+
| ||
| D、无法确定 |
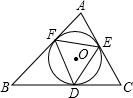 如图,△ABC中,内切圆O和边BC、CA、AB分别相切于点D、E、F,则以下四个结论中,错误的结论是( )
如图,△ABC中,内切圆O和边BC、CA、AB分别相切于点D、E、F,则以下四个结论中,错误的结论是( )| A、点O是△DEF的外心 | ||
B、∠AFE=
| ||
C、∠BOC=90°+
| ||
D、∠DFE=90°一
|
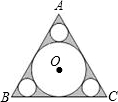 如图,已知正三角形ABC的边长为6,在△ABC中作内切圆O及三个角切圆(我们把与角两边及三角形内切圆都相切的圆叫角切圆),则△ABC的内切圆O的面积为
如图,已知正三角形ABC的边长为6,在△ABC中作内切圆O及三个角切圆(我们把与角两边及三角形内切圆都相切的圆叫角切圆),则△ABC的内切圆O的面积为 41、如图所示,△ABC中,内切圆I和边BC,CA,AB分别相切于点D,E,F,若∠FDE=70°,求∠A的度数.
41、如图所示,△ABC中,内切圆I和边BC,CA,AB分别相切于点D,E,F,若∠FDE=70°,求∠A的度数. 如图,△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,则∠FDE与∠A的关系是( )
如图,△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,则∠FDE与∠A的关系是( )