题目内容
 如图,△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,则∠FDE与∠A的关系是( )
如图,△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,则∠FDE与∠A的关系是( )分析:根据切线的性质得出∠AFI=∠AEI=90°,进而得出∠A+∠EIF=180°,即可得出
∠A+
∠FIE=90°,进而得出答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:连接FI,IE,
解:连接FI,IE,
∵△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,
∴∠AFI=∠AEI=90°,
∴∠A+∠EIF=180°,
∵∠FDE=
∠FIE,
∴
∠A+
∠FIE=90°,
∴
∠A+∠FDE=90°.
故选:C.
 解:连接FI,IE,
解:连接FI,IE,∵△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,
∴∠AFI=∠AEI=90°,
∴∠A+∠EIF=180°,
∵∠FDE=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
故选:C.
点评:此题主要考查了切线的性质以及四边形内角和定理、圆周角定理等知识,根据已知得出∠A+∠EIF=180°是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
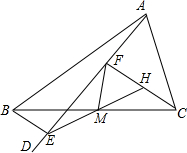 如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,延长CH交AD于F,则下列结论错误的是( )
如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,延长CH交AD于F,则下列结论错误的是( )| A、BM=CM | ||
B、FM=
| ||
| C、CF⊥AD | ||
| D、FM⊥BC |
 9、如图,△ABC中,AB=AC,∠BAC=40°,D为△ABC内一点,如果将△ACD绕点A按逆时针方向旋转到△ABD′的位置,则∠ADD′的度数是( )
9、如图,△ABC中,AB=AC,∠BAC=40°,D为△ABC内一点,如果将△ACD绕点A按逆时针方向旋转到△ABD′的位置,则∠ADD′的度数是( ) (2012•北辰区一模)如图,△ABC中,∠A=50°,点E、F在AB、AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于( )
(2012•北辰区一模)如图,△ABC中,∠A=50°,点E、F在AB、AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于( ) 如图,△ABC中,已知AB=AC,△DEF是△ABC的内接正三角形,α=∠BDF,β=∠CED,γ=∠AFE,则用β、γ表示α的关系式是
如图,△ABC中,已知AB=AC,△DEF是△ABC的内接正三角形,α=∠BDF,β=∠CED,γ=∠AFE,则用β、γ表示α的关系式是 如图,△ABC中,∠BAC=60°,AB=2AC.点P在△ABC内,且PA=
如图,△ABC中,∠BAC=60°,AB=2AC.点P在△ABC内,且PA=