题目内容
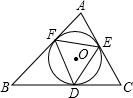 如图,△ABC中,内切圆O和边BC、CA、AB分别相切于点D、E、F,则以下四个结论中,错误的结论是( )
如图,△ABC中,内切圆O和边BC、CA、AB分别相切于点D、E、F,则以下四个结论中,错误的结论是( )| A、点O是△DEF的外心 | ||
B、∠AFE=
| ||
C、∠BOC=90°+
| ||
D、∠DFE=90°一
|
分析:首先连接如图所示的辅助线.采用排除法,证明A、B、C选项,从而错误的选择D.在证明中运用弦切角定理,直角三角形的两直角边所对的角互余.
解答: 解:A、∵点O是△ABC的内心
解:A、∵点O是△ABC的内心
∴OE=OD=OF
∴点O也是△DEF的外心
∴该选项正确;
B、∵∠AFE=∠EDF(弦切角定理)
在Rt△BOD中,∠BOD=90°-∠OBD=90°-
∠B
同理∠COD=90°-
∠C
∴∠BOC=∠BOD+∠COD=180°-
(∠C+∠B),即∠BOC=180°-
(∠C+∠B)
在四边形MOND中,
?∠BOC+∠MDN=180°?∠MDN=180°-∠BOC,即∠BOC=180°-∠EDF
∴∠AFE=
(∠B+∠C)
故该选项正确;
C、∵∠AFE=∠EDF(弦切角定理),
∵在Rt△AFO中,∠AFE=90°-∠FAO=90°-
∠A,
由上面B选项知∠MDN=180°-∠BOC=180°-(90°-
∠A)=90°+
∠A,
故该选项正确;
故选D.
 解:A、∵点O是△ABC的内心
解:A、∵点O是△ABC的内心∴OE=OD=OF
∴点O也是△DEF的外心
∴该选项正确;
B、∵∠AFE=∠EDF(弦切角定理)
在Rt△BOD中,∠BOD=90°-∠OBD=90°-
| 1 |
| 2 |
同理∠COD=90°-
| 1 |
| 2 |
∴∠BOC=∠BOD+∠COD=180°-
| 1 |
| 2 |
| 1 |
| 2 |
在四边形MOND中,
|
∴∠AFE=
| 1 |
| 2 |
故该选项正确;
C、∵∠AFE=∠EDF(弦切角定理),
∵在Rt△AFO中,∠AFE=90°-∠FAO=90°-
| 1 |
| 2 |
由上面B选项知∠MDN=180°-∠BOC=180°-(90°-
| 1 |
| 2 |
| 1 |
| 2 |
故该选项正确;
故选D.
点评:本题考查三角形内切圆与内心、三角形外接圆与外心、弦切角定理.同学们需注意对于选择题目,采用排除法是一种很好的方法.

练习册系列答案
相关题目
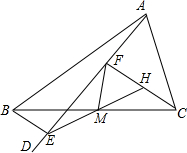 如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,延长CH交AD于F,则下列结论错误的是( )
如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,延长CH交AD于F,则下列结论错误的是( )| A、BM=CM | ||
B、FM=
| ||
| C、CF⊥AD | ||
| D、FM⊥BC |
 9、如图,△ABC中,AB=AC,∠BAC=40°,D为△ABC内一点,如果将△ACD绕点A按逆时针方向旋转到△ABD′的位置,则∠ADD′的度数是( )
9、如图,△ABC中,AB=AC,∠BAC=40°,D为△ABC内一点,如果将△ACD绕点A按逆时针方向旋转到△ABD′的位置,则∠ADD′的度数是( ) (2012•北辰区一模)如图,△ABC中,∠A=50°,点E、F在AB、AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于( )
(2012•北辰区一模)如图,△ABC中,∠A=50°,点E、F在AB、AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于( ) 如图,△ABC中,已知AB=AC,△DEF是△ABC的内接正三角形,α=∠BDF,β=∠CED,γ=∠AFE,则用β、γ表示α的关系式是
如图,△ABC中,已知AB=AC,△DEF是△ABC的内接正三角形,α=∠BDF,β=∠CED,γ=∠AFE,则用β、γ表示α的关系式是 如图,△ABC中,∠BAC=60°,AB=2AC.点P在△ABC内,且PA=
如图,△ABC中,∠BAC=60°,AB=2AC.点P在△ABC内,且PA=