题目内容
如图，E为正方形ABCD内一点，∠AEB=135°，△AEB按顺时针方向旋转一个角度后成为△CFB，图中考点：旋转的性质
专题：
分析：根据旋转的定义可知旋转中心为点B，旋转角为90°，由旋转的性质可知△BEF为等腰直角三角形，利用勾股定理可求得EF．
解答：解：由△AEB按顺时针方向旋转一个角度后成为△CFB，
∴旋转中心为点B，且旋转角为90°，
∴△BEF为等腰直角三角形，
∵BE=1，
∴由勾股定理可求得EF=
，
故答案为：点B；
．
∴旋转中心为点B，且旋转角为90°，
∴△BEF为等腰直角三角形，
∵BE=1，
∴由勾股定理可求得EF=
| 2 |
故答案为：点B；
| 2 |
点评：本题主要考查旋转的性质，掌握旋转图形为全等形是解题的关键，注意勾股定理的应用．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
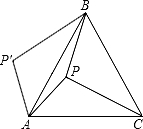如图，P是正△ABC内的一点，若将△PAC绕点A逆时针旋转到△P′AB，
请把下列各数在数轴上表示出来，然后用“＜”连接．
已知：如图，△ABC的外接圆⊙O，弦BC的长为4，∠A=30°，求圆心O到BC的距离．
2011年冬，中国出现了大范围的降温天气，某气象研究中心观测到西伯利亚寒流：开始一段时间寒流速度平均每小时增加2千米；4小时后，寒流经过开阔平原，速度变为平均每小时增加4千米，然后速度保持不变；当寒流遇到山地，速度y（千米/小时）与时间x（小时）成反比例关系，慢慢减弱，如图所示，请结合图象，解答下列问题：