题目内容
 如图,直线l:y=-
如图,直线l:y=-| 3 |
| 4 |
(1)求OA、OB的长;
(2)当S△ABP=
| 1 |
| 3 |
(3)若以P、Q、A为顶点的三角形与△ABO全等(不与△ABO重合),请求出所有符合条件的直线PQ的解析式.
考点:一次函数综合题
专题:
分析:(1)分别令y=0,x=0可求出OA和OB的长;
(2)可求出△ABO的面积,由条件可知△OBP的面积是△ABO面积的
,设出P的坐标,表示出OP的长度,可求得P点坐标;
(3)由条件可知△APQ为直角三角形,A点不可能为直角顶点,分P和Q为直角顶点两种情况讨论,再由全等得到线段相等,可求出P点的坐标,进一步可求出直线PQ的解析式.
(2)可求出△ABO的面积,由条件可知△OBP的面积是△ABO面积的
| 2 |
| 3 |
(3)由条件可知△APQ为直角三角形,A点不可能为直角顶点,分P和Q为直角顶点两种情况讨论,再由全等得到线段相等,可求出P点的坐标,进一步可求出直线PQ的解析式.
解答:解:
(1)令y=0,解得x=12,所以OA=12,令x=0,解得y=9,所以OB=9;
(2)S△ABO=
AO•BO=
×12×9=54,由S△ABP=
S△ABO=18,
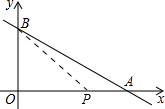
设P点的坐标为(x,0),由题意可知P点应该在x轴的正半轴,所以OP=x,则AP=|x-12|,则S△ABP=
•AP•OB=
×9×|x-12|=
|x-12|=18,解得x=8或16,所以P点的坐标为(8,0)或(16,0);
(3)由条件可知△APQ为直角三角形,A点不可能为直角顶点,
当P为直角顶点时,过P作x轴的垂线,此时有AP=AO=12,所以P点的坐标为(0,0)(与△AOB重合,舍去)或(24,0),此时直线PQ的解析式为x=24,
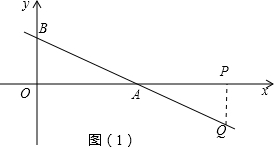
当Q为直角顶点时,过P作PQ垂直直线l,垂足为Q,由OA=12,OB=9,可求得AB=15,由全等可得PA=AB=15,所以P点的坐标为(-3,0)或(27,0)

因为直线l的斜率为-
,所以直线PQ的斜率为
,
当P点坐标为(-3,0)时,直线PQ的解析式为:y=
(x+3),即y=
x+4,
当P点坐标为(27,0)时,直线PQ的解析式为:y=
(x-27),即y=
x-36,
综上可知满足条件的直线PQ的解析式为x=24或y=
x+4或y=
x-36.
(1)令y=0,解得x=12,所以OA=12,令x=0,解得y=9,所以OB=9;
(2)S△ABO=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |

设P点的坐标为(x,0),由题意可知P点应该在x轴的正半轴,所以OP=x,则AP=|x-12|,则S△ABP=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
(3)由条件可知△APQ为直角三角形,A点不可能为直角顶点,
当P为直角顶点时,过P作x轴的垂线,此时有AP=AO=12,所以P点的坐标为(0,0)(与△AOB重合,舍去)或(24,0),此时直线PQ的解析式为x=24,

当Q为直角顶点时,过P作PQ垂直直线l,垂足为Q,由OA=12,OB=9,可求得AB=15,由全等可得PA=AB=15,所以P点的坐标为(-3,0)或(27,0)

因为直线l的斜率为-
| 3 |
| 4 |
| 4 |
| 3 |
当P点坐标为(-3,0)时,直线PQ的解析式为:y=
| 4 |
| 3 |
| 4 |
| 3 |
当P点坐标为(27,0)时,直线PQ的解析式为:y=
| 4 |
| 3 |
| 4 |
| 3 |
综上可知满足条件的直线PQ的解析式为x=24或y=
| 4 |
| 3 |
| 4 |
| 3 |
点评:本题主要考查一次函数解析式的求法及全等三角形的性质的应用,解题的关键是求得P点的坐标.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
已知α为锐角,下列不等式中正确的是( )
①tanα>1;②0<sinα<1;③cotα<1;④0<cosα<1.
①tanα>1;②0<sinα<1;③cotα<1;④0<cosα<1.
| A、② | B、①,②,③ |
| C、②,④ | D、①,②,③,④ |
下列说法:①等腰三角形的高、中线、角平分线互相重合;②等腰三角形的两腰上的中线长相等;③等腰三角形的腰一定大于其腰上的高;④等腰三角形的一边长为8,一边长为16,那么它的周长是32或40.其中不正确的( )
| A、①③ | B、①④ |
| C、①③④ | D、①②③④ |
一条线段的黄金分割点有( )
| A、1个 | B、2个 | C、3个 | D、无数个 |
下列函数中,是二次函数的为( )
| A、y=ax3+x2+bx+c(a≠0) | ||
B、y=x2+
| ||
| C、y=(x+1)2-x2 | ||
| D、y=x(1-x) |
