题目内容
已知,如图,矩形ABCD中,E是CD的中点,连接BE并延长BE交AD的延长线于点F,连接AE.
(1)求证:AD=DF;
(2)若AD=3,AE⊥BE,求AB的长.


【考点】矩形的性质;全等三角形的判定与性质;勾股定理.
【专题】几何综合题.
【分析】(1)根据E是CD的中点,BC∥AF可确定EF=EB,从而得出△EBC≌△EFD,继而得出结论.
(2)由(1)得出的EF=EB,结合AE⊥BE可得AB=AF,从而根据AD=3可得出答案.
【解答】解:(1)∵BC∥AF,E是CD的中点,
∴E是线段FB的中点,
∴FE=EB,
又∠FED=∠BEC,DE=EC,
∴△EBC≌△EFD,
∴AD=DF.
(2)由(1)得:EF=EB,
又AE⊥BE,
∴AB=AF(中垂线的性质)
∴AB=AF=2AD=6.
【点评】本题考查了矩形的性质及勾股定理的知识,有一定的难度,解答本题的关键是根据题意得出E是FB的中点,这是本题的突破口.

练习册系列答案
相关题目


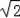
 ≈1.414,
≈1.414,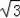


 x
x



 的图象与x轴的交点坐标是_________,与y轴的交点坐标是__________.
的图象与x轴的交点坐标是_________,与y轴的交点坐标是__________.