题目内容
1.化简求值:$\frac{2y}{{x}^{2}-2xy+{y}^{2}}$÷($\frac{1}{x-y}$-$\frac{1}{x+y}$),其中x=$\sqrt{2}$+1,y=$\sqrt{2}$-1.分析 先算括号里面的,再算除法,最后把x、y的值代入进行计算即可.
解答 解:原式=$\frac{2y}{(x-y)^{2}}$÷$\frac{x+y-x+y}{(x+y)(x-y)}$
=$\frac{2y}{{(x-y)}^{2}}$÷$\frac{2y}{(x+y)(x-y)}$
=$\frac{2y}{{(x-y)}^{2}}$•$\frac{(x+y)(x-y)}{2y}$
=$\frac{x+y}{x-y}$.
当x=$\sqrt{2}$+1,y=$\sqrt{2}$-1时,原式=$\frac{\sqrt{2}+1+\sqrt{2}-1}{\sqrt{2}+1-\sqrt{2}+1}$=$\frac{2\sqrt{2}}{2}$=$\sqrt{2}$.
点评 本题考查的是分式的化简求值,在解答此类题目时要注把结果化为最简分式,再求值.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
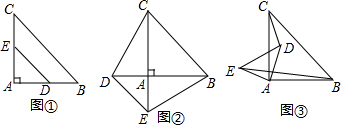
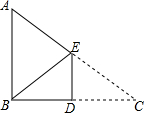 如图,有一张直角三角形纸片ABC,边AB=6,AC=10,∠ABC=90°,将该直角三角形纸片沿DE折叠,使点C与点B重合,则四边形ABDE的周长为( )
如图,有一张直角三角形纸片ABC,边AB=6,AC=10,∠ABC=90°,将该直角三角形纸片沿DE折叠,使点C与点B重合,则四边形ABDE的周长为( ) 如图,Rt△ABO中,∠AOB=90°,∠ABO=30°,点A在第二象限,点B在第一象限,过点A的反比例函数表达式为y=-$\frac{1}{x}$,则过点B的反比例函数表达式为y=$\frac{3}{x}$.
如图,Rt△ABO中,∠AOB=90°,∠ABO=30°,点A在第二象限,点B在第一象限,过点A的反比例函数表达式为y=-$\frac{1}{x}$,则过点B的反比例函数表达式为y=$\frac{3}{x}$.