题目内容
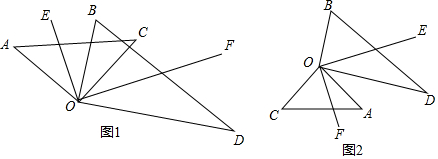
2.将一副三角板分别按图1和图2的位置摆放,其中直角顶点重合,OE平分∠AOB,OF平分∠COD.(1)图1中∠AOB与∠COD的关系为相等,理由是同角的余角相等;
(2)求图1中∠EOF的度数;
(3)图2中∠EOF的度数变化吗?若不变,请说明理由,若变化,请求出此时∠EOF的度数.
分析 (1)根据余角的性质即可得到结论;
(2)根据角平分线的定义得到∠BOE=$\frac{1}{2}∠$AOB,∠DOF=$\frac{1}{2}∠$COD,得到∠BOE=∠DOF,等量代换得到结论;
(3)根据角平分线的性质得到∠AOE=$\frac{1}{2}∠$AOB,∠COF=$\frac{1}{2}∠$COD,求得∠AOE=∠COF,等量代换得到结论.
解答 解:(1)相等,
理由:∵∠AOC=∠BOD=90°,
∴∠AOB+∠BOC=∠COD+∠BOC=90°,
∴∠AOB=∠COD;
故答案为:相等;
(2)∵OE平分∠AOB,OF平分∠COD,
∴∠BOE=$\frac{1}{2}∠$AOB,∠DOF=$\frac{1}{2}∠$COD,
∵∠AOB=∠COD,
∴∠BOE=∠DOF,
∵∠EOF=∠BOE+∠BOC+∠COF=∠DOF+∠COF+∠BOC=90°;
(3)不变,
理由:∵OE平分∠AOB,OF平分∠COD,
∴∠AOE=$\frac{1}{2}∠$AOB,∠COF=$\frac{1}{2}∠$COD,
∵∠AOB=∠COD,
∴∠AOE=∠COF,
∵∠EOF=∠AOE+∠AOF=∠COF+∠AOF=90°.
点评 本题考查了余角的性质,角平分线的定义,正确的识别图形是解题的关键.

练习册系列答案
相关题目
12.实数-π,-3.14,0,$\sqrt{2}$四个数中,最小的是( )
| A. | -π | B. | -3.14 | C. | $\sqrt{2}$ | D. | 0 |
13.下列从左边到右边的变形,属于因式分解的是( )
| A. | (2-x)(2+x)=4-x2 | B. | -a(a-b)=-a2+ab | C. | m2-n2=(m+n)(m-n) | D. | (1-x)2=(x-1)2 |
17.下列各式中,计算正确的是( )
| A. | x(2x-1)=2x2-1 | B. | x2-9=(x-3)( x+3 ) | C. | (a+2)2=a2+4 | D. | (x+2)(x-3)=x2+x-6 |
7.无理数$\sqrt{31}$在哪两个整数之间( )
| A. | 15与16 | B. | 4与5 | C. | 5与6 | D. | 6与7 |
14.餐桌边的一蔬一饭,舌尖上的一饮一啄,来之不易,舌尖上的浪费让人触目惊心,据统计,中国每年浪费的食物总量折合粮食约500亿千克,这个数据用科学记数法表示为( )
| A. | 50×109千克 | B. | 5×1010千克 | C. | 5×1011千克 | D. | 0.5×1012千克 |
10.下列说法中,不正确的是( )
| A. | 圆的周长与它的半径之比是一个不变的常数 | |
| B. | 圆的面积与它的半径之比是一个不变的常数 | |
| C. | 圆周率是一个确定的值,它的准确值是π,它是一个无限不循环小数 | |
| D. | 圆周率是一个确定的值,它的一个近似值是3.14 |
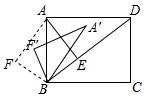 如图,矩形ABCD中,AB=2,AD=2$\sqrt{3}$,AE⊥BD,垂足是E,点F是点E关于AB的对称点,连接AF、BF,将△ABF绕点B顺时针旋转一个α(90°<α<180°)记旋转中的△ABF为△A′B′F′,在旋转过程中,设A′F′所在的直线与直线AD交于点P,与直线BD交于点Q,若△DPQ是等腰三角形,且DP=DQ,则DQ的长为4-$\sqrt{6}$+$\sqrt{2}$.
如图,矩形ABCD中,AB=2,AD=2$\sqrt{3}$,AE⊥BD,垂足是E,点F是点E关于AB的对称点,连接AF、BF,将△ABF绕点B顺时针旋转一个α(90°<α<180°)记旋转中的△ABF为△A′B′F′,在旋转过程中,设A′F′所在的直线与直线AD交于点P,与直线BD交于点Q,若△DPQ是等腰三角形,且DP=DQ,则DQ的长为4-$\sqrt{6}$+$\sqrt{2}$.