题目内容
5.解分式方程:$\frac{3}{{x}^{2}-9}$-$\frac{x}{3-x}$=1.分析 分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:去分母得:3+x(x+3)=x2-9,
解得:x=-4,
检验:把x=-4代入(x+3)(x-3)≠0,
则x=-4是原分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
15.已知一个布袋里装有5个红球,3个白球,这些球除颜色外其余都相同.从该布袋里任意摸出1个球,若第一次是1个白球不放回,则第二次摸出白球的概率( )
| A. | $\frac{3}{8}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{28}$ | D. | $\frac{9}{64}$ |
20.计算(a3)2•a2的结果是( )
| A. | a7 | B. | a8 | C. | a10 | D. | a11 |
14.将6.18×10-3化为小数是( )
| A. | 0.000618 | B. | 0.00618 | C. | 0.0618 | D. | 0.618 |
15.计算a•a-1的结果为( )
| A. | -1 | B. | 0 | C. | 1 | D. | -a |
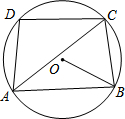 如图,四边形ABCD为⊙O的内接四边形,连接AC、BO,已知∠CAB=36°,∠ABO=30°,则∠D=96°.
如图,四边形ABCD为⊙O的内接四边形,连接AC、BO,已知∠CAB=36°,∠ABO=30°,则∠D=96°.