题目内容
2.已知点A、B坐标分别为(0,2)和(3,0),则AB=$\sqrt{13}$(保留根号)分析 在平面直角坐标系中标出点A、点B,利用勾股定理,即可解答.
解答 解:如图,
∵A、B坐标分别为(0,2)和(3,0),
∴OA=2,OB=3,
在Rt△AOB中,AB=$\sqrt{O{A}^{2}+O{B}^{2}}=\sqrt{{2}^{2}+{3}^{2}}=\sqrt{13}$.
故答案为:$\sqrt{13}$.
点评 本题考查了坐标与图形性质,解决本题的关键是根据坐标的性质,利用勾股定理进行解答.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
17.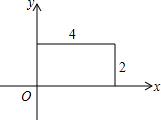 如图,一个矩形的两边长分别是4和2,建立直角坐标系,则下列不在矩形上的点为( )
如图,一个矩形的两边长分别是4和2,建立直角坐标系,则下列不在矩形上的点为( )
 如图,一个矩形的两边长分别是4和2,建立直角坐标系,则下列不在矩形上的点为( )
如图,一个矩形的两边长分别是4和2,建立直角坐标系,则下列不在矩形上的点为( )| A. | (4,0) | B. | (2,4) | C. | (0,2) | D. | (4,2) |
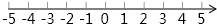
 在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$的图象经过点A(1,4),B(m,n).
在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$的图象经过点A(1,4),B(m,n). 如图,已知点A(1,1),B(4,1),则线段AB上任意一点的坐标可表示为y=1(1≤x≤4).
如图,已知点A(1,1),B(4,1),则线段AB上任意一点的坐标可表示为y=1(1≤x≤4). 【问题情境】反比例函数y=$\frac{2}{x}$和y=$\frac{8}{x}$在平面直角坐标系xOy第一象限的图象如图所示,点A在y=$\frac{8}{x}$的图象上,AB∥y轴,与y=$\frac{2}{x}$的图象交于点B,AC、BD与x轴平行,分别与y=$\frac{2}{x}$、y=$\frac{8}{x}$的图象交于点C、D.点A、B、C、D的纵坐标分别记为yA、yB、yC、yD,记点A的横坐标为m(m>0).
【问题情境】反比例函数y=$\frac{2}{x}$和y=$\frac{8}{x}$在平面直角坐标系xOy第一象限的图象如图所示,点A在y=$\frac{8}{x}$的图象上,AB∥y轴,与y=$\frac{2}{x}$的图象交于点B,AC、BD与x轴平行,分别与y=$\frac{2}{x}$、y=$\frac{8}{x}$的图象交于点C、D.点A、B、C、D的纵坐标分别记为yA、yB、yC、yD,记点A的横坐标为m(m>0). 已知△ABC三个顶点的坐标分别是 A(-3,-1)、B(1,3)、C(2,-3)
已知△ABC三个顶点的坐标分别是 A(-3,-1)、B(1,3)、C(2,-3)