题目内容
2.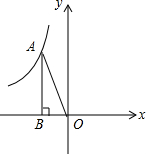 如图,反比例函数y=$\frac{k}{x}$在第二象限的图象上有一点A,过点A作AB⊥x轴于B,且S△AOB=2,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$在第二象限的图象上有一点A,过点A作AB⊥x轴于B,且S△AOB=2,则k的值为( )| A. | -4 | B. | 2 | C. | -2 | D. | 4 |
分析 先根据反比例函数图象所在的象限判断出k的符号,再根据S△AOB=2求出k的值即可.
解答 解:∵反比例函数的图象在二、四象限,
∴k<0,
∵S△AOB=2,
∴|k|=4,
∴k=-4,即可得双曲线的表达式为:y=-$\frac{4}{x}$,
故选A.
点评 本题考查的是反比例系数k的几何意义,即在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{|k|}{2}$,且保持不变.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
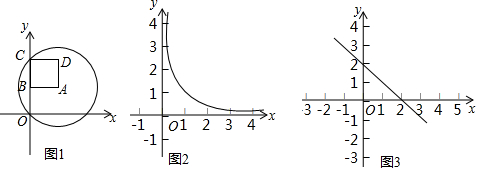
13.如图1,在△ABC中,AB=AC,∠BAC=120°.点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为x,图1中某条线段的长为y,若表示y与x的函数关系的大致图象如图2所示,则这条线段可能是图1中的( )


| A. | BD | B. | AD | C. | OD | D. | CD |
10. 如图,已知AD∥BE∥CF,$\frac{AB}{BC}$=$\frac{2}{3}$,DE=3,则DF的长为( )
如图,已知AD∥BE∥CF,$\frac{AB}{BC}$=$\frac{2}{3}$,DE=3,则DF的长为( )
 如图,已知AD∥BE∥CF,$\frac{AB}{BC}$=$\frac{2}{3}$,DE=3,则DF的长为( )
如图,已知AD∥BE∥CF,$\frac{AB}{BC}$=$\frac{2}{3}$,DE=3,则DF的长为( )| A. | 2 | B. | 4.5 | C. | 3 | D. | 7.5 |
11.下列四个数在-2和1之间的数是( )
| A. | 0 | B. | -3 | C. | 2 | D. | 3 |
 如图,在矩形ABCD中,对角线AC、BD相交于O,AE⊥BD于点E,已知AB=3,AD=3$\sqrt{3}$,求△AEO的面积.
如图,在矩形ABCD中,对角线AC、BD相交于O,AE⊥BD于点E,已知AB=3,AD=3$\sqrt{3}$,求△AEO的面积.